|
Binary (0/1) ensemble |
OP = OPBINARY(M,N,MODE) creates an M by N binary ensemble
operator. When choosing MODE = 0 an explicit binary matrix is
formed and used when applying the operator. Choosing MODE = 1
causes the operator to generate the above matrix on the fly,
each time the operator is used. This mode can be used when
dealing with very large matrices.
|
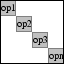 |
Operator-diagonal operator |
OPBLOCKDIAG(WEIGHTS, OP1, OP2, ...) creates a compound
operator with the given weighted operators on the diagonal;
DIAG([WEIGHT1*OP1, WEIGHT2*OP2, ...]). The WEIGHT parameter is
optional and can either be a scalar or a vector. In case of a
scalar, all operators are weighted equally. If only a single
operator is given it is replicated as many times as there are
weights.
See also opFoG, opKron, opWindowedOp, opDictionary.
|
 |
Two-dimensional blurring operator |
OPBLUR(M,N) creates an blurring operator for M by N
images. This function is used for the GPSR-based test problems
and is based on the implementation by Figueiredo, Nowak and
Wright, 2007.
This operator may soon be replaced by opConvolve2d.
|
 |
Restriction operator on matrix columns |
OPCOLUMNRESTRCIT(M,N,IDX,TYPE), with TYPE = 'DISCARD', creates
an operator that extracts the columns indicated by IDX from a
given M by N matrix. The adjoint operator takes an M by
length(IDX) matrix and outputs an M by N matrix with the
columns filled by the given input matrix. Note that all input
and output matrices are in vectorized from. When TYPE =
'ZERO', all columns that are not in IDX are zero-padded
instead of discarded.
See also opMask, opRestriction.
|
 |
One-dimensional convolution operator |
OPCONVOLVE1D(KERNEL,OFFSET,CIRCULAR) creates a one-dimensional
convolution operator with the KERNEL function. The length of
the KERNEL vector must coincide with the signal length. OFFSET
gives the index in the KERNEL vector to be taken as its
center and is set to 1 by default (i.e. no shifting). The
CIRCULAR flag indicates whether the signal is periodic. If set
to any non-zero value convolution is wrapped around the vector
endpoints. By default CIRCULAR is set to 1.
|
 |
Two-dimensional curvelet operator |
OPCURVELET2D(M,N,NBSCALES,NBANGLES,TTYPE) creates a
two-dimensional curvelet operator for M by N matrices. The
curvelet transform is computed using the Curvelab code.
The remaining three parameters are optional; NBSCALES gives
the number of scales and is set to ceil(log2(min(M,N)) - 3)
by default, as suggested by Curvelab. NBANGLES gives the number
of angles at the second coarsest level which must be a
multiple of four with a minimum of 8. By default NBANGLES is
set to 16. TTYPE determines the type of transformation and is
set to 'WRAP' by default.
See also CURVELAB.
|
 |
One-dimensional discrete cosine transform (DCT) |
OPDCT(N) creates a one-dimensional discrete cosine transform
operator for vectors of length N.
|
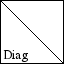 |
Scaling operator (i.e., diagonal matrix). |
OPDIAG(N,D) creates an operator for N by N diagonal matrix
multiplication. The diagonal is given by D which can be either
a vector of length N or a scalar. OPDIAG(D) is a shortcut for
OPDIAG(LENGTH(D),D) and can be used instead.
|
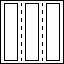 |
Dictionary of concatenated operators |
OPDICTIONARY(WEIGHTS, OP1, OP2, ...) creates a dictionary
operator consisting of the concatenation of all operators;
[WEIGHT1*OP1 | WEIGHT2*OP2 | ...]. The WEIGHT parameter is
optional and can either be a scalar or a vector. In case of a
scalar, all operators are weighted equally.
See also opFoG, opBLockDiag.
|
 |
Identity operator |
OPDIRAC(N) creates the identity operator for vectors of length
N.
|
 |
One-dimensional fast Fourier transform (FFT). |
OPFFT(N) create a one-dimensional normalized Fourier transform
operator for vectors of length N.
|
 |
Centralized two-dimensional fast Fourier transform (FFT). |
OPFFT2C(M,N) creates a two-dimensional normalized Fourier
Transform that operates on matrices of size M by N. The
components are shifted to have to zero-frequency component in
the center of the spectrum.
|
 |
Two-dimensional fast Fourier transform (FFT) |
OPFFT2D(M,N) creats a two-dimensional normalized Fourier
transform operator for matrices of size M by N. Input and
output of the matrices is done in vectorized form.
|
 |
Concatenate a sequence of operators into a single operator. |
OPFOG(OP1,OP2,...OPn) creates an operator that successively
applies each of the operators OP1, OP2, ..., OPn on a given
input vector. In non-adjoint mode this is done in reverse
order, starting with OPn.
See also opDictionary
|
 |
Gaussian ensemble |
OPGAUSSIAN(M,N,MODE) creates an M by N Gaussian ensemble
operator. By setting MODE a number of different types of
ensemble can be generated; MODE = 0 (default) explicitly
creates an unnormalized matrix from the Normal
distribution. MODE = 1 generates columns of the unnormalized
matrix as the operator is applied. This allows for much larger
ensembles since the matrix is implicit. For MODE = 2,3 columns
are scaled to have unit Euclidean norm, when MODE = 3 the
matrix is implicit. For MODE 4,5,6 the rows are orthogonalized
using respectively the QR, ORTH and SVD functions. For the
last three modes matrices are always generated
explicitly. The orthogonalization modes work only when M < N.
|
 |
One-dimensional Haar wavelet |
OPHAAR(N,LEVELS) creates a Haar wavelet operator for one
dimensional signal of length N. LEVELS indicates the number of
scales to use, default is 5.
See also opWavelet
|
 |
Two-dimensional Haar wavelet |
OPHAAR2D(N,LEVELS) creates a Haar wavelet operator for two
dimensional signal of size M by N. LEVELS indicates the number of
scales to use, default is 5.
See also opWavelet
|
 |
Hadamard matrix |
OPHADAMARD(N,NORMALIZED) creates a Hadamard operator for
vectors of length N. When N is not a power of two, vectors are
internally padded by zeroes to the next power of
two. Multiplication is done using a fast recursive
implementation. When the normalized flag is set, the columns
of the Hadamard matrix are scaled to unit two-norm. By default
the NORMALIZED flag is set to 0.
|
 |
Heaviside operator |
OPHEAVISIDE(N,S) creates an operator for multiplication by an
N by N Heaviside matrix. These matrices have ones below and on
the diagonal and zeros elsewhere. S is a flag indicating
whether the columns should be scaled to unit Euclidean
norm. By default the columns are unnormalized.
|
 |
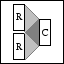
Kronecker tensor product |
OPKRON(OP1,OP2) creates an operator that is the Kronecker
tensor product of OP1 and OP2.
|
 |
Selection mask |
OPMASK(A) creates an operator that computes the dot-product of
a given vector with the (binary) mask provided by A. If A is a
matrix it will be vectorized prior to use.
See also opColRestrict, opRestriction.
|
 |
Apply arbitrary matrix as operator. |
OPMATRIX(A,OPINFO) creates an operator that performs
matrix-vector multiplication with matrix A. Optional parameter
OPINFO can be used to override the default operator
information returned when querying the operator, or provide a
string giving the interpretation of the matrix. When OPINFO is
a cell array the first entry is the operator name followed by
additional information for that operator type (this option is
mostly provided for internal use by other operators).
|
 |
Padding operator |
OPPADDING(SIZELHS,SIZERHS) create an operator that pads and
unpads matrices equally around each size. SIZELHS and SIZERHS
give the matrix size before and after padding. SIZERHS must
be greater than or equal to SIZELHS, and both must have an even
number of rows and columns.
|
 |
Discard imaginary components |
OPREAL(N) creates an operator that discards the imaginary
components of input vectors of length N.
|
 |
Restriction operator |
OPRESTRICTION(N,IDX) creates a restriction operator that
selects the entries listed in IDX from an input vector of
length N. The adjoint of the operator creates a vector of
length N and fills the entries given by IDX with the input
data.
See also opColumnRestriction, opMask.
|
 |
Sign-ensemble operator. |
OPSIGN(M,N,MODE) creates an M by N sign-ensemble operator. By
setting MODE a number of different types of ensemble can be
generated; MODE = 0 (default) explicitly creates an
unnormalized matrix with random +1 and -1 entries. MODE = 1
generates columns of the unnormalized matrix as the operator
is applied. This allows for much larger ensembles since the
matrix is implicit. For MODE = 2,3 columns are scaled to have
unit Euclidean norm, when MODE = 3 the matrix is implicit.
|
 |
Complex to real and imaginary |
OPSPLITCOMPLEX(N) creates a nonlinear operator that splits a
complex vector of length N into its real and imaginary parts
[real(x); imag(x)]. In transpose mode it combines the real and
imaginary parts into a complex vector.
|
 |
Transpose operator |
OPTRANSPOSE(OP) creates an operator that is the the adjoint
operator OP.
|
 |
Wavelet operator |
OPWAVELET(M,N,FAMILY,FILTER,LEVELS,TYPE) creates a wavelet
operator of given FAMILY, for M by N matrices. The wavelet
transformation is computed using the Rice Wavelet Toolbox.
The remaining three parameters are optional. FILTER = 8
specifies the filter length and must be even. LEVELS = 5 gives
the number of levels in the transformation. Both M and N must
be divisible by 2^LEVELS. TYPE = 'min' indictates what type of
solution is desired; 'min' for minimum phase, 'max' for
maximum phase, and 'mid' for mid-phase solutions.
|
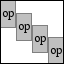 |
Overcomplete windowed operator |
OPWINDOWEDOP(M,OPERATOR,WINDOW,OVERLAP) creates an
overcomplete windowed operator with overlap:
/ +------------+-------------------------+
| | | |
| | Diag(W)*OP | |
| | +------------+ | --
M / +------------+ | | -- OVERLAP
\ | | Diag(W)*OP | |
| | | +------------+
| | +------------+ |
| | | Diag(W)*OP |
\ +-------------------------+------------+
with W for WINDOW and OP for OPERATOR.
Parameter OVERLAP must be strictly less than the length of
WINDOW, which in turn must coincide with the number of rows
in the OPERATOR. M indicates the signal length and prescribes
the number of rows in the resulting operator. The number of
columns is always an integer multiple of the number of columns
in OPERATOR and depends on the required number of blocks.
|