Contents
% a simple demo of how to do structure learning with data from a DBN
Demo configuration
rand('seed',0); % Deterministic randomness randn('seed',0); HMM = 1; HUSMEIER = 2; dbnType = HUSMEIER;
Create a DBN
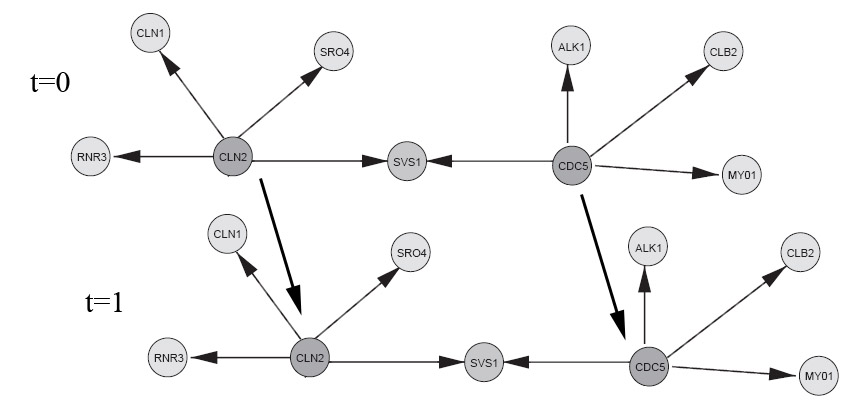
if dbnType == HMM elseif dbnType == HUSMEIER; % Reproduced from a subset of the network from figure 3, Husmeier. % "Sensitivity and specificity of inferring genetic % regulatory interactions from microarray experiments with dynamic % Bayesian networks". Bioinformatics, Vol. 19 no. 17 2003, pages % 2271–2282. % See "husmeier_network.jpg" image in Demos directory to see network % topology (compare to Husmeier, figure 3). % show the ground truth groundTruthImage = imread('husmeier_network.jpg'); figure('Position',[100 100 size(groundTruthImage,2) size(groundTruthImage,1)]); image(groundTruthImage); axis('image'); axis('off'); set(gca,'Position',[0 0 1 1]) title('Husmeier ground truth'); % With this choice of inter-slice connections, we can expect to learn % the full casual bayes-net with observational-only data (assuming the % sampled parameters induce a faithful distribution). CLN2 = 1; CDC5 = 2; RNR3 = 3; SRO4 = 6; CLN1 = 4; SVS1 = 5; ALK1 = 7; CLB2 = 8; MY01 = 9; % There appears to be a bug in BNT mk_bnet automatically sorts nodes in topological order, while mk_dbn % does not (on the intra adjacency matrix) % From Husmeier's paper intra = zeros(9); intra(CLN2,CLN1)=1; intra(CLN2,SRO4)=1; intra(CLN2,SVS1)=1; intra(CLN2,RNR3)=1; intra(CDC5,SVS1)=1; intra(CDC5,ALK1)=1; intra(CDC5,CLB2)=1; intra(CDC5,MY01)=1; % Add some arbitrarily chosen inter-slice edges inter = zeros(9); inter(CLN2,CLN2)=1; inter(CDC5,CDC5)=1; dnodes = 1:9; bnet = mk_dbn(intra, inter, 2*ones(1,9), 'discrete', dnodes); % sample parameters for the network bnet = myMkBnet( length(bnet.CPD), bnet.node_sizes(:), 'bnet', bnet, 'method', 'meek'); maxFanIn = 4; nData = 5000; end
Sample data from the DBN
data = cell2mat(sample_dbn(bnet, 'length', nData )); % sample some data from the DBN
Convert the data representation to one suitable for direct input into the BNSL routines
Transform the sampled data into a format suitable for BNSL (from time-series to time-slices) Returns a struct holding the new (doubled) # of nodes, a layering that encodes the flow of time, and the transformed data.
dataDbn = transformDbnData(data, 'maxFanIn', maxFanIn); % *** Important function
Learn the DBN back with the DP algorithm
Since all the parameters are randomly sampled, they could lead to a non-faithful distrubtion (ie. one that encodes conditionally independences not encoded by the DBN).
% These are the same functions used in simpleDemo.m (they are used throughout the BNSL package) aflp = mkAllFamilyLogPrior( dataDbn.nNodes, 'nodeLayering', dataDbn.nodeLayering, 'maxFanIn', dataDbn.maxFanIn); aflml = mkAllFamilyLogMargLik( dataDbn.data, 'nodeArity', bnet.node_sizes(:), 'impossibleFamilyMask', aflp~=-Inf, 'verbose', 1); ep = computeAllEdgeProb( aflp, aflml); % There is no point in doing structure learning on the first time step, since % we cannot learn anything from a single data point (in terms of posterior features, such as edges) % aflp = mkAllFamilyLogPrior( dataDbn.nNodes ); % aflml = mkAllFamilyLogMargLik( data(:,1), 'nodeArity', 2*ones(1,2)); % ep0 = computeAllEdgeProb( aflp, aflml);
Node 1/18 Node 2/18 Node 3/18 Node 4/18 Node 5/18 Node 6/18 Node 7/18 Node 8/18 Node 9/18 Node 10/18 Node 11/18 Node 12/18 Node 13/18 Node 14/18 Node 15/18 Node 16/18 Node 17/18 Node 18/18
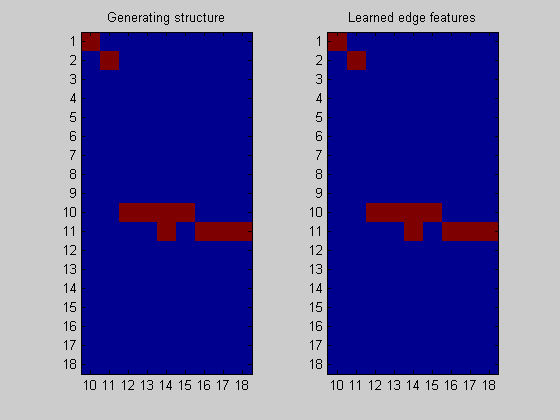
Plot the result
nNodes = length(bnet.intra); figure; subplot(1,2,1); imagesc(bnet.dag(:,nNodes+1:end)); title('Generating structure'); axis('equal'); axis('tight'); set(gca,'ytick',1:dataDbn.nNodes); set(gca,'xtick',1:nNodes); set(gca,'xticklabel',nNodes+1:size(bnet.dag,2)); subplot(1,2,2); imagesc(ep(:,nNodes+1:end),[0 1]); title('Learned edge features'); axis('equal'); axis('tight'); set(gca,'ytick',1:dataDbn.nNodes); set(gca,'xtick',1:nNodes); set(gca,'xticklabel',nNodes+1:size(bnet.dag,2));