Speedup tricks

One of the main disadvantages of matlab compared to compiled languages such as C is that it can be much slower. However, there are a few simple tricks that can make a big difference to the speed of your matlab code. We discuss some of these below.

Contents

The danger of premature optimization

Before spending a lot of time optimizing your code, you should first identify the key bottlenecks using the profiler. The usual pattern is that 80% of the the time is spend in 20% of the code, so you can focus your efforts accordingly. Also, remember that correctness is more important than speed!

Profiling your code

Matlab has an excellent profiler, which can tell you how much time your code spends in each one of its functions. It automatically generates a web page summarizing the results, which you can click on to 'drill down'. See the example below.

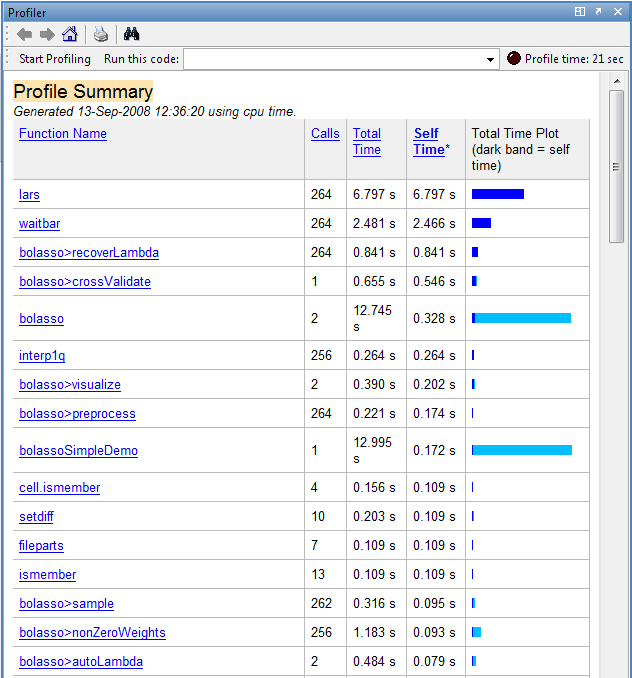
The report shows a breakdown of all the functions called from your function, the number of times they were called, and the total time spent executing them. Self-time, denoted by a dark blue band, is the the time spent within a function not including how long was spent in functions called from here. This is really the statistic you should pay attention to. You can click on a function name to bring up its sourcecode.

You can turn on profiling with the profile on command and turn it off again with profile off. Once profiling is on, execute your code, and then type profile viewer to see the report.

Timing code

The profiler tells you where all the time is being spent, but maybe you just want to know how much time your code is taking. The simplest way to time code is to call tic before your code starts and toc afterwards. A more reliable method is the timeit function, which calls tic/toc multiple times and averages. Matlab used to have a flops command, but it was removed. Tom Minka has written some flop counting routines as part of his lightspeed package.

Progress bar

We can print a graphical bar that indicates how long a certain operation has taken/ will take, as in this example.

w = waitbar(0,'My Progress Bar');                       % create a new waitbar, w with 0% progress
for i=1:500
   isprime(i);
   w = waitbar(i/500,w,['iteration: ',num2str(i)]);     % update the wait bar each iteration
end
close(w);                                               % remember to close it

Memory preallocation

Matlab stores matrices in contiguous blocks of memory. When the size of a matrix changes, Matlab, if it has not preallocated enough space, must find a new chunk of memory large enough and copy the matrix over. When a matrix grows inside of a loop, this process may have to be repeated over and over again causing huge delays. It can therefore significantly speed up your code by preallocating a chunk of memory before entering into a loop. The zeros() command is the most common way to do this. Below we see two simple loops in which we store the numbers 1 to 30 000. We preallocate only in the second. Timing the two loops with the tic() and toc() commands we see that preallocating in this case speeds up the code by about 30 times. The larger the matrices, the more important this becomes. 

tic
for i = 1:30000
    A(i) = i;
end
without = toc

without =
    3.6559

tic
B = zeros(30000,1);      % Preallocate B with the zeros command.
for i = 1:30000
    B(i) = i;
end
with = toc
ratio = without / with

with =
    0.0315
ratio =
  116.2151

Vectorization

Vectorization is the process of making your code work on array-structured data in parallel, rather than using for-loops. This can make your code much faster and is an essential skill to learn. We give various examples below which should give you some good idioms to copy. Many more examples can be found here.

Using built-in functions which are vectorized

Most functions in Matlab are already vectorized. For example, to take the log of every number in an array A, we simply execute B = log(A). Let us compare this vectorized version to calling log on each element. 

A = rand(200,200);                    % We will use this as our data

non-vectorized version

tic                                   % time the code
Bnv = zeros(size(A));                 % We preallocate to level the playing field
for i=1:size(A,1)
    for j=1:size(A,2);
        Bnv(i,j) = log(A(i,j));
    end
end
nonvec = toc;

vectorized version

tic
Bv = log(A);
vec = toc;
assert(isequal(Bnv,Bv));
ratio = nonvec / vec

ratio =
    7.6243

Some functions, like mvnpdf() for example, interpret an n-by-d matrix, not as n-times-d elements but as n, d-dimensional vectors. If this is not what we are after, we can convert the matrix into a vector using the (:) operator, pass it to the function, and reshape the output back into the original size with the reshape() function.

Logical indexing.

Here we see the benefit of logical indexing in making code shorter, faster and easier to read.

non-vectorized version

tic
B1 = [];                                % note, it is difficult to preallocate here
counter = 1;
 for j=1:size(A,2)
     for i=1:size(A,1)
        if(A(i,j) < 0.2)
            B1(counter,1) = A(i,j);
            counter = counter + 1;
        end
    end
end
nonvec = toc;

vectorized version

tic
B2 = A(A < 0.2);
vec = toc;
ratio = nonvec / vec
assert(isequal(B1,B2));

ratio =
  256.6016

A slightly more complex example of vectorization

Here we perform three tricks at once as it were. Recall that operators such as ^, \, have element-wise equivalents, (e.g. .^), which we can apply to the corresponding elements of two same-sized matrices. Secondly, Matlab performs automatic scalar expansion in expressions like A+1, and thirdly, we can easily multiply two matrices together without loops. Most loops involving patterned additions and multiplications of vector elements can be translated, with a little thought, into equivalent vectorized statements.

non-vectorized version

tic
B1 = zeros(size(A));
for i=1:size(A,1)
    for j=1:size(A,2)
       T = 0;
       for k=1:size(A,1)
           T = T + A(i,k)*A(j,k);
       end
       B1(i,j) = T * (A(i,j)/2) + 1;
    end
end
nonvec = toc;

vectorized version

tic
B2 = ((A*A') .* (A/2)) + 1;
vec = toc;
test = mean(abs(B1(:) - B2(:))) % very small differences between B1, & B2 because of numerical error
ratio = nonvec / vec

test =
  3.4905e-015
ratio =
  109.2798

Bsxfun

One often finds it necessary to subtract say a row vector from a matrix, (e.g. perhaps you want to standardize your data). Since the row vector is neither a scalar, nor the same size as the matrix, Matlab will not let you do this directly. One option is to use the repmat() function we saw earlier to replicate the vector so that it is the same size as the matrix and then subtract. However, a better option is to use the bsxfun() function (bsx stands for binary singleton expansion). You must first specify the operation you wish to perform preceded by the @ symbol. Typical choices include @minus, @plus, @times, @rdivide (however, any binary function can be used - type doc bsxfun for a list). Next the arguments to the function are specified, beginning with the argument whose size does not need to be changed: bsxfun then expands any singleton dimensions in the third argument to the correct size. This function supports multidimensional arrays. 

A = meshgrid(1:6,1:5)'
B = A - repmat(mean(A,1),size(A,1),1);     % center each column
C = bsxfun(@minus, A, mean(A,1))           % center each column (the better way)
check = isequal(B,C)
D =  bsxfun(@rdivide,A,sqrt(sum(A.^2,1)))  % make each column have unit norm

A =
     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4
     5     5     5     5     5
     6     6     6     6     6
C =
   -2.5000   -2.5000   -2.5000   -2.5000   -2.5000
   -1.5000   -1.5000   -1.5000   -1.5000   -1.5000
   -0.5000   -0.5000   -0.5000   -0.5000   -0.5000
    0.5000    0.5000    0.5000    0.5000    0.5000
    1.5000    1.5000    1.5000    1.5000    1.5000
    2.5000    2.5000    2.5000    2.5000    2.5000
check =
     1
D =
    0.1048    0.1048    0.1048    0.1048    0.1048
    0.2097    0.2097    0.2097    0.2097    0.2097
    0.3145    0.3145    0.3145    0.3145    0.3145
    0.4193    0.4193    0.4193    0.4193    0.4193
    0.5241    0.5241    0.5241    0.5241    0.5241
    0.6290    0.6290    0.6290    0.6290    0.6290

Bsxfun vs repmat

For a detailed timing comparison of bsxfun and repmat, see performance here. Below we just give a simple example. We subtract off the mean of the third dimension and leave our 'non-vectorized' version at least somewhat vectorized to emphasize the role of bsxfun(). 

A3d = rand(100,100,100);
A1 = A3d; A2 = A3d; A3 = A3d;

non-vectorized version

tic
m = mean(A1,3);
for i=1:size(A1,3)
   A1(:,:,i) = A1(:,:,i) - m;
end
nonvec = toc

nonvec =
    0.0457

vectorized version

tic
A2 = bsxfun(@minus,A2,mean(A2,3));
vec = toc

vec =
    0.0162

We could have also used repmat() as follows, but this requires more memory and is slightly slower. 

tic
A3 = A3 - repmat(mean(A3,3),[1,1,size(A3,3)]);
rep = toc

rep =
    0.0266

assert(isequal(A1,A2,A3));

Example using mat2cell and cellfun

Suppose we have a large numeric matrix and we want to apply a function to arbitrary sized blocks of it. That is, we want to partition a matrix of size m-by-n into many smaller matrices of differing sizes, apply a function to each block, and group the results back together. We could extract each block first with a long series of indexing operations and then loop over them all applying the function, but there is better way involving the mat2cell() and cellfun() functions, discussed in this section

A = rand(100,40);                               % here is our data

Partition the matrix into 12 blocks of different sizes. These blocks are stored in a 4x3 cell array. Notice the sizes of each of the 12 blocks and how we achieved these sizes with the inputs to mat2cell(). 

groups = mat2cell(A,[10,30,20,40],[5,27,8])

groups = 
    [10x5 double]    [10x27 double]    [10x8 double]
    [30x5 double]    [30x27 double]    [30x8 double]
    [20x5 double]    [20x27 double]    [20x8 double]
    [40x5 double]    [40x27 double]    [40x8 double]

Create a function to apply to each block; we will choose something simple like replacing each element in a block with the block's largest value. 

f = @(x)repmat(max(x(:)),size(x));

Use the cellfun() function to apply this function to every one of the 12 elements in groups, (i.e. to every matrix block). We have to set 'UniformOutput' to false because the sizes of the elements returned by cellfun() will be different. 

groupSums = cellfun(f,groups,'UniformOutput',false)

groupSums = 
    [10x5 double]    [10x27 double]    [10x8 double]
    [30x5 double]    [30x27 double]    [30x8 double]
    [20x5 double]    [20x27 double]    [20x8 double]
    [40x5 double]    [40x27 double]    [40x8 double]

We then convert back to a numeric matrix with the same size as our original matrix A.

B = cell2mat(groupSums);

See also the filter2 command. If you have the image processing toolbox, check out the blkproc and im2col commands, which are similar.

More speedup tips

In the last example, we used cellfun() function but there is a similar function arrayfun() that applies a function to every element of an array. When other vectorization techniques fail, this can be a better alternative than looping over every element yourself.

The vectorize() function takes in a string or function handle and converts all operators, (e.g ^) to their element-wise equivalents, (e.g. .^). This can be useful when using someone else's function that was not vectorized to begin with.

Recall from the matrix chapter that there are many functions that will create matrices for such as meshgrid(), or blkdiag(), yet again helping us avoid loops.

When a value vec(i) depends on on entries v(1)...v(i-1) for instance, we can use functions like cumsum(), cumprod(), filter(), conv(), and accumarray(). See their help entries for more information.

Tom Minka has some tips, and references to other people's tips, here.

Compiling matlab

Details on how to compile matlab to standalone code, using mcc, can be found here. Note, however, that this does not usually result in a speed increase: the purpose of mcc is to make code that can run without matlab, which it does by generating byte code which is interpreted by a matlab virtual machine.

There is a method called emlmex that does give speedups, but only for a very narrow set of functions. In particular, every time the size of the memory footprint of the function changes, it must be recompiled.

The only way to get really big speedup is to implement your code in another language like C, compile it with mex, and then call that code from within your Matlab program. For details, click here.


Published with MATLAB® 7.8