Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
12.6.1 Using Definite Clauses for Context-Free Grammars
This section shows how to use definite clauses to represent aspects of the syntax and semantics of natural language.
Languages are defined by their legal sentences. Sentences are sequences of symbols. The legal sentences are specified by a grammar.
Our first approximation of natural language is a context-free grammar. A context-free grammar is a set of rewrite rules, with non-terminal symbols transforming into a sequence of terminal and non-terminal symbols. A sentence of the language is a sequence of terminal symbols generated by such rewriting rules. For example, the grammar rule
sentence→noun_phrase, verb_phrase
means that a non-terminal symbol sentence can be a noun_phrase followed by a verb_phrase. The symbol "→" means "can be rewritten as." If a sentence of natural language is represented as a list of words, this rule means that a list of words is a sentence if it is a noun phrase followed by a verb phrase:
sentence(S)←noun_phrase(N), verb_phrase(V),append(N,V,S).
To say that the word "computer" is a noun, you would write
noun([computer]).
There is an alternative, simpler representation of context-free grammar rules using definite clauses that does not require an explicit append, known as a definite clause grammar (DCG). Each non-terminal symbol s becomes a predicate with two arguments, s(T1,T2), which means that list T2 is an ending of the list T1 such that all of the words in T1 before T2 form a sequence of words of the category s. Lists T1 and T2 together form a difference list of words that make the class given by the non-terminal symbol, because it is the difference of these that forms the syntactic category.
The atomic symbol
[passed,the,course,with,a,computer])
is true in the intended interpretation because "the student" forms a noun phrase.
The grammar rule
sentence→noun_phrase, verb_phrase
means that there is a sentence between some T0 and T2 if there exists a noun phrase between T0 and T1 and a verb phrase between T1 and T2:

This grammar rule can be specified as the following clause:
noun_phrase(T0,T1) ∧
verb_phrase(T1,T2).
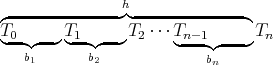
In general, the rule
says that h is composed of a b1 followed by a b2, ..., followed by a bn, and is written as the definite clause
b1(T0,T1)∧
b2(T1,T2)∧
...
bn(Tn-1,Tn).
using the interpretation
where the Ti are new variables.
To say that non-terminal h gets mapped to the terminal symbols, t1,...,tn, one would write
h([t1,···,tn|T],T)
using the interpretation
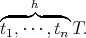
Thus, h(T1,T2) is true if T1=[t1,...,tn|T2].
h →a, b, [c, d], e, [f], g
and can be represented as
a(T0,T1)∧
b(T1,[c,d|T3])∧
e(T3,[f|T5])∧
g(T5,T6).
Note that the translations T2=[c,d|T3] and T4=[f|T5] were done manually.
% A sentence is a noun phrase followed by a verb phrase.
noun_phrase(T0,T1)∧
verb_phrase(T1,T2).
% A noun phrase is a determiner followed by modifiers followed by a noun followed by an optional prepositional phrase.
det(T0,T1)∧
modifiers(T1,T2)∧
noun(T2,T3)∧
pp(T3,T4).
% Modifiers consist of a (possibly empty) sequence of adjectives.
modifiers(T0,T2)←
adjective(T0,T1) ∧
modifiers(T1,T2).
% An optional prepositional phrase is either nothing or a preposition followed by a noun phrase.
pp(T0,T2)←
preposition(T0,T1) ∧
noun_phrase(T1,T2).
%
A verb phrase is a verb followed by a noun phrase and an
optional
prepositional phrase.
verb(T0,T1)∧
noun_phrase(T1,T2)∧
pp(T2,T3).
det([a|T],T).
det([the|T],T).
noun([student|T],T).
noun([course|T],T).
noun([computer|T],T).
adjective([practical|T],T).
verb([passed|T],T).
preposition([with|T],T).
Figure 12.6 axiomatizes a simple grammar of English. Figure 12.7 gives a simple dictionary of words and their parts of speech, which can be used with this grammar.
ask noun_phrase([the,student,passed,the,course,with,a,computer],R).
will return
R=[passed,the,course,with,a,computer].
The sentence "The student passed the course with a computer." has two different parses, one using the clause instance
verb([passed,the,course,with,a,computer],
[the,course,with,a,computer])∧
noun_phrase([the,course,with,a,computer],[])∧
pp([],[])
and one using the instance
verb([passed,the,course,with,a,computer],
[the,course,with,a,computer])∧
noun_phrase([the,course,with,a,computer],[with,a,computer])∧
pp([with,a,computer],[]).
In the first of these, the prepositional phrase modifies the noun phrase (i.e., the course is with a computer); and in the second, the prepositional phrase modifies the verb phrase (i.e., the course was passed with a computer).



