Contents
- Linear Regression on the Simplex
- Lasso regression
- Lasso with Complex Variables
- Group-Sparse Linear Regression with Categorical Features
- Group-Sparse Simultaneous Regression
- Group-Sparse Multinomial Logistic Regression
- Group-Sparse Multi-Task Classification
- Low-Rank Multi-Task Classification
- L_1,inf Blockwise-Sparse Graphical Lasso
- L_1,2 Blockwise-Sparse Graphical Lasso
- Linear Regression with the Over-Lasso
- Kernelized dual form of support vector machines
- Smooth (Primal) Support Vector Machine with Multiple Kernel Learning
- Conditional Random Field Feature Selection
- Approximating node marginals in undirected graphical models with variational mean field
- Multi-State Markov Random Field Structure Learning
- Conditional Random Field Structure Learning with Pseudo-Likelihood
Linear Regression on the Simplex
We will solve min_w |Xw-y|^2, s.t. w >= 0, sum(w)=1
Projection onto the simplex can be computed in O(n log n), this is described in (among other places): Michelot. A Finite Algorithm for Finding the Projection of a Point onto the Canonical Simplex of R^n. Journal of Optimization Theory and Applications (1986).
% Generate Syntehtic Data nInstances = 50; nVars = 10; X = randn(nInstances,nVars); w = rand(nVars,1).*(rand(nVars,1) > .5); y = X*w + randn(nInstances,1); % Initial guess of parameters wSimplex = zeros(nVars,1); % Set up Objective Function funObj = @(w)SquaredError(w,X,y); % Set up Simplex Projection Function funProj = @(w)projectSimplex(w); % Solve with PQN fprintf('\nComputing optimal linear regression parameters on the simplex...\n'); wSimplex = minConf_PQN(funObj,wSimplex,funProj); % Check if variable lie in simplex wSimplex' fprintf('Min value of wSimplex: %.3f\n',min(wSimplex)); fprintf('Max value of wSimplex: %.3f\n',max(wSimplex)); fprintf('Sum of wSimplex: %.3f\n',sum(wSimplex)); pause
Computing optimal linear regression parameters on the simplex...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 2.92731e-03 1.04820e+02 8.97365e-01
2 3 14 1.00000e+00 6.71088e+01 5.65136e-01
3 4 22 1.00000e+00 6.70715e+01 2.00314e-01
4 5 30 1.00000e+00 6.70711e+01 2.61336e-03
5 6 35 1.00000e+00 6.70711e+01 1.01669e-04
Directional Derivative below progTol
ans =
Columns 1 through 7
0.2474 0 0 0.2932 0.4594 0 0
Columns 8 through 10
0 0 0
Min value of wSimplex: 0.000
Max value of wSimplex: 0.459
Sum of wSimplex: 1.000
Lasso regression
We will solve min_w |Xw-y|^2 s.t. sum_i w_i <= tau
Projection onto the L1-Ball can be computed in O(n), see: Duchi, Shalev-Schwartz, Singer, and Chandra. Efficient Projections onto the L1-Ball for Learning in High Dimensions. ICML (2008).
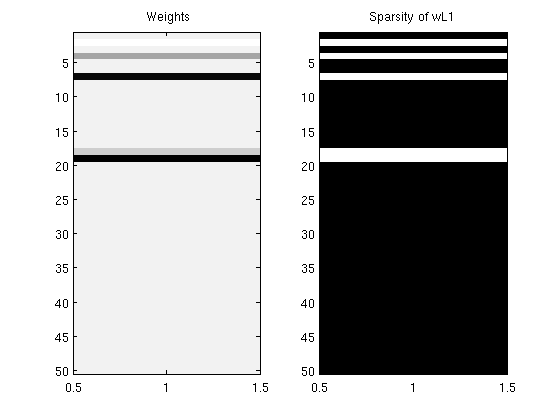
% Generate Syntehtic Data nInstances = 500; nVars = 50; X = randn(nInstances,nVars); w = randn(nVars,1).*(rand(nVars,1) > .5); y = X*w + randn(nInstances,1); % Initial guess of parameters wL1 = zeros(nVars,1); % Set up Objective Function funObj = @(w)SquaredError(w,X,y); % Set up L1-Ball Projection tau = 2; funProj = @(w)sign(w).*projectRandom2C(abs(w),tau); % Solve with PQN fprintf('\nComputing optimal Lasso parameters...\n'); wL1 = minConf_PQN(funObj,wL1,funProj); wL1(abs(wL1) < 1e-4) = 0; % Check sparsity of solution wL1' fprintf('Number of non-zero variables in solution: %d (of %d)\n',nnz(wL1),length(wL1)); figure; subplot(1,2,1); imagesc(wL1);colormap gray; title(' Weights'); subplot(1,2,2); imagesc(wL1~=0);colormap gray; title('Sparsity of wL1'); pause
Computing optimal Lasso parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 3.69062e-05 1.58865e+04 1.99993e+00
2 3 15 1.00000e+00 1.19915e+04 1.29253e+00
3 4 24 1.00000e+00 1.19883e+04 1.23647e+00
4 5 32 1.00000e+00 1.19882e+04 2.62204e-01
5 6 39 1.00000e+00 1.19882e+04 3.76125e-02
6 7 45 1.00000e+00 1.19882e+04 1.08715e-03
Directional Derivative below progTol
ans =
Columns 1 through 7
0 0.0526 0 -0.2532 0 0 -0.7711
Columns 8 through 14
0 0 0 0 0 0 0
Columns 15 through 21
0 0 0 -0.1177 -0.8054 0 0
Columns 22 through 28
0 0 0 0 0 0 0
Columns 29 through 35
0 0 0 0 0 0 0
Columns 36 through 42
0 0 0 0 0 0 0
Columns 43 through 49
0 0 0 0 0 0 0
Column 50
0
Number of non-zero variables in solution: 5 (of 50)
Lasso with Complex Variables
We will solve min_w |Xz-y|^2, s.t. sum_i z_i <= tau, where z and y are complex, and z represents the complex modulus
Efficient projection onto this complex L1-Ball is described in: van den Berg and Friedlander. Probing the Pareto Frontier for Basis Pursuit Solutions. SIAM Journal of Scientific Computing (2008).
The calculation of the projection can be reduced from the O(n log n) required in the above to O(n) by using a linear-time median finding algorithm
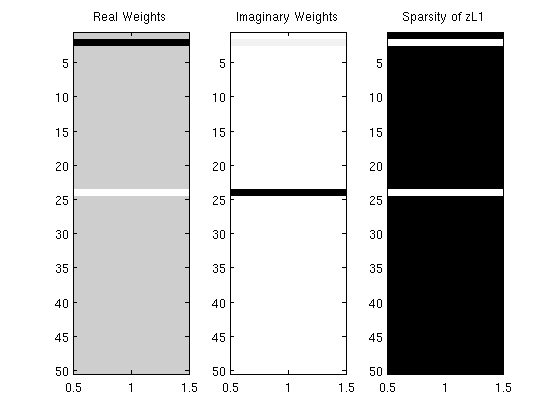
% Generate Syntehtic Data nInstances = 500; nVars = 50; X = randn(nInstances,nVars); z = complex(randn(nVars,1),randn(nVars,1)).*(rand(nVars,1) > .5); y = X*z; % Initial guess of parameters zReal = zeros(nVars,1); zImag = zeros(nVars,1); % Set up Objective Function funObj = @(zRealImag)SquaredError(zRealImag,[X zeros(nInstances,nVars);zeros(nInstances,nVars) X],[real(y);imag(y)]); % Set up Complex L1-Ball Projection tau = 2; funProj = @(zRealImag)complexProject(zRealImag,tau); % Solve with PQN fprintf('\nComputing optimal Lasso parameters...\n'); zRealImag = minConf_PQN(funObj,[zReal;zImag],funProj); zReal = zRealImag(1:nVars); zImag = zRealImag(nVars+1:end); zL1 = complex(zReal,zImag); zL1(abs(zL1) < 1e-4) = 0; figure subplot(1,3,1); imagesc(zReal);colormap gray; title('Real Weights'); subplot(1,3,2); imagesc(zImag);colormap gray; title('Imaginary Weights'); subplot(1,3,3); imagesc(zL1~=0);colormap gray; title('Sparsity of zL1'); % Check sparsity of solution zL1' fprintf('Number of non-zero variables in solution: %d (of %d)\n',nnz(zL1),length(zL1)); pause
Computing optimal Lasso parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 2.48486e-05 2.25735e+04 1.99850e+00
2 3 13 1.00000e+00 1.72665e+04 7.89444e-01
3 4 20 1.00000e+00 1.72652e+04 1.24561e+00
4 5 27 1.00000e+00 1.72652e+04 1.25796e-02
5 6 33 1.00000e+00 1.72652e+04 2.99222e-04
Directional Derivative below progTol
ans =
Columns 1 through 4
0 -1.2442 + 0.0335i 0 0
Columns 5 through 8
0 0 0 0
Columns 9 through 12
0 0 0 0
Columns 13 through 16
0 0 0 0
Columns 17 through 20
0 0 0 0
Columns 21 through 24
0 0 0 0.2936 + 0.6959i
Columns 25 through 28
0 0 0 0
Columns 29 through 32
0 0 0 0
Columns 33 through 36
0 0 0 0
Columns 37 through 40
0 0 0 0
Columns 41 through 44
0 0 0 0
Columns 45 through 48
0 0 0 0
Columns 49 through 50
0 0
Number of non-zero variables in solution: 2 (of 50)
Group-Sparse Linear Regression with Categorical Features
We will solve min_w |Xw-y|^2, s.t. sum_g |w_g|_inf <= tau, where X uses binary indicator variables to represent a set of categorical features, and we use the 'groups' g to encourage sparsity in terms of the original categorical variables
Using the L_1,inf mixed-norm for group-sparsity is described in: Turlach, Venables, and Wright. Simultaneous Variable Selection. Technometrics (2005).
Using group sparsity to select for categorical variables encoded with indicator variables is described in: Yuan and Lin. Model Selection and Estimation in Regression with Grouped Variables. JRSSB (2006).
Projection onto the L_1,inf mixed-norm ball can be computed in O(n log n), this is described in: Quattoni, Carreras, Collins, and Darell. An Efficient Projection for l_{1,\infty} Regularization. ICML (2009).
% Generate categorical features nInstances = 100; nStates = [3 3 3 3 5 4 5 5 6 10 3]; % Number of discrete states for each categorical feature X = zeros(nInstances,length(nStates)); offset = 0; for i = 1:nInstances for s = 1:length(nStates) prob_s = rand(nStates(s),1); prob_s = prob_s/sum(prob_s); X(i,s) = sampleDiscrete(prob_s); end end % Make indicator variable encoding of categorical features X_ind = zeros(nInstances,sum(nStates)); clear w for s = 1:length(nStates) for i = 1:nInstances X_ind(i,offset+X(i,s)) = 1; end w(offset+1:offset+nStates(s),1) = (rand > .75)*randn(nStates(s),1); offset = offset+nStates(s); end y = X_ind*w + randn(nInstances,1); % Initial guess of parameters w_ind = zeros(sum(nStates),1); % Set up Objective Function funObj = @(w)SquaredError(w,X_ind,y); % Set up groups offset = 0; groups = zeros(size(w_ind)); for s = 1:length(nStates) groups(offset+1:offset+nStates(s),1) = s; offset = offset+nStates(s); end % Set up L_1,inf Projection Function tau = .05; funProj = @(w)groupLinfProj(w,tau,groups); % Solve with PQN fprintf('\nComputing Group-Sparse Linear Regression with Categorical Features Parameters...\n'); w_ind = minConf_PQN(funObj,w_ind,funProj); w_ind(abs(w_ind) < 1e-4) = 0; % Check selected variables w_ind' for s = 1:length(nStates) fprintf('Number of non-zero variables associated with categorical variable %d: %d (of %d)\n',s,nnz(w_ind(groups==s)),sum(groups==s)); end fprintf('Total number of categorical variables selected: %d (of %d)\n',nnz(accumarray(groups,abs(w_ind))),length(nStates)); pause
Computing Group-Sparse Linear Regression with Categorical Features Parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 6.75309e-04 4.02268e+02 4.99662e-02
2 3 9 1.00000e+00 3.88459e+02 0.00000e+00
First-Order Optimality Conditions Below optTol
ans =
Columns 1 through 7
0 0 0 0 0 0 0
Columns 8 through 14
0 0 -0.0500 0.0500 0.0500 0 0
Columns 15 through 21
0 0 0 0 0 0 0
Columns 22 through 28
0 0 0 0 0 0 0
Columns 29 through 35
0 0 0 0 0 0 0
Columns 36 through 42
0 0 0 0 0 0 0
Columns 43 through 49
0 0 0 0 0 0 0
Column 50
0
Number of non-zero variables associated with categorical variable 1: 0 (of 3)
Number of non-zero variables associated with categorical variable 2: 0 (of 3)
Number of non-zero variables associated with categorical variable 3: 0 (of 3)
Number of non-zero variables associated with categorical variable 4: 3 (of 3)
Number of non-zero variables associated with categorical variable 5: 0 (of 5)
Number of non-zero variables associated with categorical variable 6: 0 (of 4)
Number of non-zero variables associated with categorical variable 7: 0 (of 5)
Number of non-zero variables associated with categorical variable 8: 0 (of 5)
Number of non-zero variables associated with categorical variable 9: 0 (of 6)
Number of non-zero variables associated with categorical variable 10: 0 (of 10)
Number of non-zero variables associated with categorical variable 11: 0 (of 3)
Total number of categorical variables selected: 1 (of 11)
Group-Sparse Simultaneous Regression
We will solve min_W |XW-Y|^2 + lambda * sum_g |W_g|_inf, where we use the 'groups' g to encourage that we select variables that are relevant across the output variables
We solve this non-differentiable problem by transforming it into the equivalent problem: min_w |XW-Y|^2 + lambda * sum_g alpha_g, s.t. forall_g alpha_g >= |W_g|_inf
Using group-sparsity to select variables that are relevant across regression tasks is described in: Turlach, Venables, and Wright. Simultaneous Variable Selection. Technometrics (2005).
The auxiliary variable formulation is described in: Schmidt, Murphy, Fung, and Rosales. Structure Learning in Random Field for Heart Motion Abnormality Detection. CVPR (2008).
Computing the projection in the auxiliary variable formulation can be done in O(n log n), this is described in the addendum of the above paper.
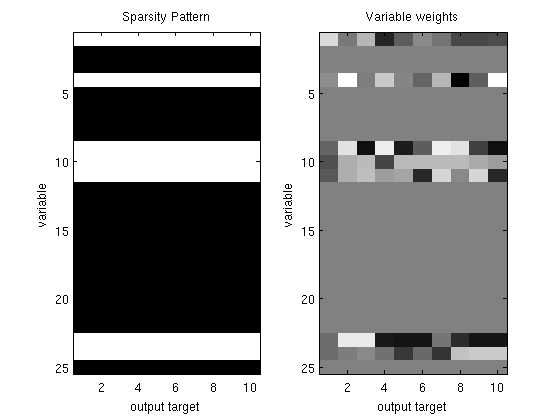
% Generate synthetic data nInstances = 100; nVars = 25; nOutputs = 10; X = randn(nInstances,nVars); W = diag(rand(nVars,1) > .75)*randn(nVars,nOutputs); Y = X*W + randn(nInstances,nOutputs); % Initial guess of parameters W_groupSparse = zeros(nVars,nOutputs); % Set up Objective Function funObj = @(W)SimultaneousSquaredError(W,X,Y); % Set up Groups groups = repmat([1:nVars]',1,nOutputs); groups = groups(:); nGroups = max(groups); % Initialize auxiliary variables that will bound norm lambda = 250; alpha = zeros(nGroups,1); penalizedFunObj = @(W)auxGroupLoss(W,groups,lambda,funObj); % Set up L_1,inf Projection Function [groupStart,groupPtr] = groupl1_makeGroupPointers(groups); funProj = @(W)auxGroupLinfProject(W,nVars*nOutputs,groupStart,groupPtr); % Solve with PQN fprintf('\nComputing group-sparse simultaneous regression parameters...\n'); Walpha = minConf_PQN(penalizedFunObj,[W_groupSparse(:);alpha],funProj); % Extract parameters from augmented vector W_groupSparse(:) = Walpha(1:nVars*nOutputs); W_groupSparse(abs(W_groupSparse) < 1e-4) = 0; figure subplot(1,2,1); imagesc(W_groupSparse~=0);colormap gray title('Sparsity Pattern'); ylabel('variable'); xlabel('output target'); subplot(1,2,2); imagesc(W_groupSparse);colormap gray title('Variable weights'); ylabel('variable'); xlabel('output target'); % Check selected variables for s = 1:nVars fprintf('Number of tasks where variable %d was selected: %d (of %d)\n',s,nnz(W_groupSparse(s,:)),nOutputs); end fprintf('Total number of variables selected: %d (of %d)\n',nnz(sum(W_groupSparse,2)),nVars); pause
Computing group-sparse simultaneous regression parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 4.22539e-05 7.06280e+03 2.19202e+02
2 3 16 1.00000e+00 3.15351e+03 2.39651e+01
3 4 28 1.00000e+00 3.10418e+03 9.86012e+00
4 5 40 1.00000e+00 3.09330e+03 2.56478e+00
5 6 52 1.00000e+00 3.09277e+03 9.42922e-01
6 7 64 1.00000e+00 3.09272e+03 3.99847e-01
7 8 76 1.00000e+00 3.09272e+03 1.76031e-01
8 9 88 1.00000e+00 3.09272e+03 4.70416e-02
9 10 99 1.00000e+00 3.09272e+03 1.24753e-02
10 11 108 1.00000e+00 3.09272e+03 3.95741e-03
11 12 115 1.00000e+00 3.09272e+03 5.25340e-04
12 13 121 1.00000e+00 3.09272e+03 2.60962e-04
Directional Derivative below progTol
Number of tasks where variable 1 was selected: 10 (of 10)
Number of tasks where variable 2 was selected: 0 (of 10)
Number of tasks where variable 3 was selected: 0 (of 10)
Number of tasks where variable 4 was selected: 10 (of 10)
Number of tasks where variable 5 was selected: 0 (of 10)
Number of tasks where variable 6 was selected: 0 (of 10)
Number of tasks where variable 7 was selected: 0 (of 10)
Number of tasks where variable 8 was selected: 0 (of 10)
Number of tasks where variable 9 was selected: 10 (of 10)
Number of tasks where variable 10 was selected: 10 (of 10)
Number of tasks where variable 11 was selected: 10 (of 10)
Number of tasks where variable 12 was selected: 0 (of 10)
Number of tasks where variable 13 was selected: 0 (of 10)
Number of tasks where variable 14 was selected: 0 (of 10)
Number of tasks where variable 15 was selected: 0 (of 10)
Number of tasks where variable 16 was selected: 0 (of 10)
Number of tasks where variable 17 was selected: 0 (of 10)
Number of tasks where variable 18 was selected: 0 (of 10)
Number of tasks where variable 19 was selected: 0 (of 10)
Number of tasks where variable 20 was selected: 0 (of 10)
Number of tasks where variable 21 was selected: 0 (of 10)
Number of tasks where variable 22 was selected: 0 (of 10)
Number of tasks where variable 23 was selected: 10 (of 10)
Number of tasks where variable 24 was selected: 10 (of 10)
Number of tasks where variable 25 was selected: 0 (of 10)
Total number of variables selected: 7 (of 25)
Group-Sparse Multinomial Logistic Regression
We will solve min_W nll(W,X,y) + lambda * sum_g |W_g|_2, where nll(W,X,y) is the negative log-likelihood in multinomial logistic regression, and where we use the 'groups' g to encourage sparsity in terms of the original input variables
We solve this non-differentiable problem by transforming it into the equivalent problem: min_W nll(W,X,y) + lambda * sum_g alpha_g, s.t. forall_g alpha_g >= |W_g|_2
Note: the bias variables are assigned to group '0', which is not penalized
Using the L_1,2 mixed-norm for group-sparsity is described in: Bakin. Adaptive Regression and Model Selection in Data Mining Problems. PhD Thesis Australian National University (1999)
Using group-sparsity to select the original input variables in multinomial classification is described in: Obozinski, Taskar, and Jordan. Joint covariate selection for grouped classification. UC Berkeley TR (2007).
The auxiliary variable formulation is described in the addendum of: Schmidt, Murphy, Fung, and Rosales. Structure Learning in Random Field for Heart Motion Abnormality Detection. CVPR (2008).
Computing the projection in the auxiliary variable formulation can be done in O(n), this is Exercise 8.3(c) of: Boyd and Vandenberghe. Convex Optimization. Cambridge University Press (2004).
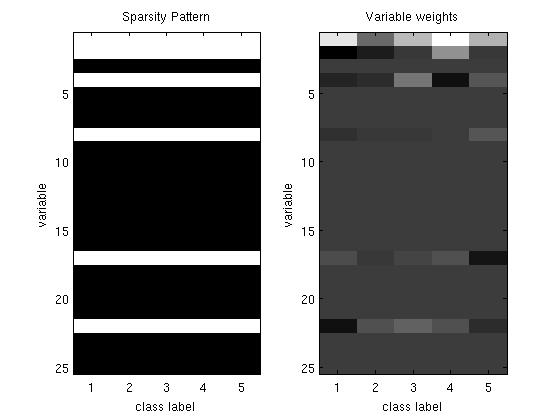
% Generate synthetic data nInstances = 100; nVars = 25; nClasses = 6; X = [ones(nInstances,1) randn(nInstances,nVars-1)]; W = diag(rand(nVars,1) > .75)*randn(nVars,nClasses); [junk y] = max(X*W + randn(nInstances,nClasses),[],2); % Initial guess of parameters W_groupSparse = zeros(nVars,nClasses-1); % Set up Objective Function funObj = @(W)SoftmaxLoss2(W,X,y,nClasses); % Set up Groups (don't penalized bias) groups = [zeros(1,nClasses-1);repmat([1:nVars-1]',1,nClasses-1)]; groups = groups(:); nGroups = max(groups); % Initialize auxiliary variables that will bound norm lambda = 10; alpha = zeros(nGroups,1); penalizedFunObj = @(W)auxGroupLoss(W,groups,lambda,funObj); % Set up L_1,2 Projection Function [groupStart,groupPtr] = groupl1_makeGroupPointers(groups); funProj = @(W)auxGroupL2Project(W,nVars*(nClasses-1),groupStart,groupPtr); % Solve with PQN fprintf('\nComputing group-sparse multinomial logistic regression parameters...\n'); Walpha = minConf_PQN(penalizedFunObj,[W_groupSparse(:);alpha],funProj); % Extract parameters from augmented vector W_groupSparse(:) = Walpha(1:nVars*(nClasses-1)); W_groupSparse(abs(W_groupSparse) < 1e-4) = 0; figure subplot(1,2,1); imagesc(W_groupSparse~=0);colormap gray title('Sparsity Pattern'); ylabel('variable'); xlabel('class label'); subplot(1,2,2); imagesc(W_groupSparse);colormap gray title('Variable weights'); ylabel('variable'); xlabel('class label'); % Check selected variables fprintf('Number of classes where bias variable was selected: %d (of %d)\n',nnz(W_groupSparse(1,:)),nClasses-1); for s = 2:nVars fprintf('Number of classes where variable %d was selected: %d (of %d)\n',s,nnz(W_groupSparse(s,:)),nClasses-1); end fprintf('Total number of variables selected: %d (of %d)\n',nnz(sum(W_groupSparse(2:end,:),2)),nVars); pause
Computing group-sparse multinomial logistic regression parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.29290e-03 1.77636e+02 1.70112e+01
2 3 16 1.00000e+00 1.35096e+02 5.41046e+00
3 4 28 1.00000e+00 1.31176e+02 2.49132e+00
4 5 40 1.00000e+00 1.30339e+02 1.17206e+00
5 6 52 1.00000e+00 1.29858e+02 1.49862e+00
6 7 64 1.00000e+00 1.29415e+02 1.00392e+00
7 8 76 1.00000e+00 1.28789e+02 7.82402e-01
8 9 87 1.00000e+00 1.28472e+02 1.55317e+00
9 10 99 1.00000e+00 1.28259e+02 5.06381e-01
10 11 110 1.00000e+00 1.28203e+02 2.35309e-01
11 12 121 1.00000e+00 1.28180e+02 1.70284e-01
12 13 132 1.00000e+00 1.28173e+02 7.28148e-02
13 14 143 1.00000e+00 1.28170e+02 3.66599e-02
14 15 153 1.00000e+00 1.28170e+02 1.09387e-02
15 16 163 1.00000e+00 1.28169e+02 1.22609e-02
16 18 174 3.59127e-01 1.28169e+02 6.22380e-03
17 19 186 1.00000e+00 1.28169e+02 2.73340e-03
18 20 197 1.00000e+00 1.28169e+02 2.83436e-03
19 21 208 1.00000e+00 1.28169e+02 4.79012e-03
20 22 219 1.00000e+00 1.28169e+02 1.02580e-03
21 23 230 1.00000e+00 1.28169e+02 1.90541e-04
22 24 241 1.00000e+00 1.28169e+02 2.52536e-04
23 25 253 1.00000e+00 1.28169e+02 6.74493e-05
Directional Derivative below progTol
Number of classes where bias variable was selected: 5 (of 5)
Number of classes where variable 2 was selected: 5 (of 5)
Number of classes where variable 3 was selected: 0 (of 5)
Number of classes where variable 4 was selected: 5 (of 5)
Number of classes where variable 5 was selected: 0 (of 5)
Number of classes where variable 6 was selected: 0 (of 5)
Number of classes where variable 7 was selected: 0 (of 5)
Number of classes where variable 8 was selected: 5 (of 5)
Number of classes where variable 9 was selected: 0 (of 5)
Number of classes where variable 10 was selected: 0 (of 5)
Number of classes where variable 11 was selected: 0 (of 5)
Number of classes where variable 12 was selected: 0 (of 5)
Number of classes where variable 13 was selected: 0 (of 5)
Number of classes where variable 14 was selected: 0 (of 5)
Number of classes where variable 15 was selected: 0 (of 5)
Number of classes where variable 16 was selected: 0 (of 5)
Number of classes where variable 17 was selected: 5 (of 5)
Number of classes where variable 18 was selected: 0 (of 5)
Number of classes where variable 19 was selected: 0 (of 5)
Number of classes where variable 20 was selected: 0 (of 5)
Number of classes where variable 21 was selected: 0 (of 5)
Number of classes where variable 22 was selected: 5 (of 5)
Number of classes where variable 23 was selected: 0 (of 5)
Number of classes where variable 24 was selected: 0 (of 5)
Number of classes where variable 25 was selected: 0 (of 5)
Total number of variables selected: 5 (of 25)
Group-Sparse Multi-Task Classification
We will solve min_W nll(W,X,Y), s.t. sum_g |W_g|_2 <= tau, where nll(W,X,Y) is the negative log-likelihood in a simultaneous binary logistic regression model, and where we use the 'groups' g to encourage that we select variables that are relevant across the binary classification tasks
Note: the bias variables are assigned to group '0', which is not penalized
Using group-sparsity to select variables that are relevant across classification tasks is described in: Obozinski, Taskar, and Jordan. Joint covariate selection for grouped classification. UC Berkeley TR (2007).
Projection onto the L_1,2 mixed-norm ball can be computed in O(n), this is described in: van den Berg, Schmidt, Friedlander, and Murphy. Group Sparsity via Linear-Time Projection. UBC TR (2008).
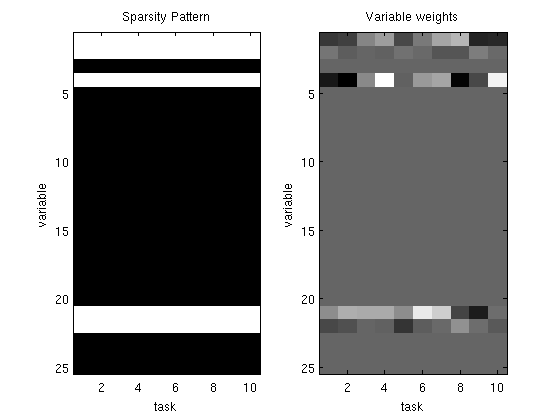
% Generate synthetic data nInstances = 100; nVars = 25; nOutputs = 10; X = [ones(nInstances,1) randn(nInstances,nVars-1)]; W = diag(rand(nVars,1) > .75)*randn(nVars,nOutputs); Y = X*W + randn(nInstances,nOutputs); % Initial guess of parameters W_groupSparse = zeros(nVars,nOutputs); % Set up Objective Function funObj = @(W)SimultaneousLogisticLoss(W,X,Y); % Set up Groups (don't penalized bias) groups = [zeros(1,nOutputs);repmat([1:nVars-1]',1,nOutputs)]; groups = groups(:); nGroups = max(groups); % Set up L_1,2 Projection Function tau = .5; funProj = @(W)groupL2Proj(W,tau,groups); % Solve with PQN fprintf('\nComputing Group-Sparse Multi-Task Classification Parameters...\n'); W_groupSparse(:) = minConf_PQN(funObj,W_groupSparse(:),funProj); W_groupSparse(abs(W_groupSparse) < 1e-4) = 0; figure subplot(1,2,1); imagesc(W_groupSparse~=0);colormap gray title('Sparsity Pattern'); ylabel('variable'); xlabel('task'); subplot(1,2,2); imagesc(W_groupSparse);colormap gray title('Variable weights'); ylabel('variable'); xlabel('task'); % Check selected variables fprintf('Number of classes where bias variable was selected: %d (of %d)\n',nnz(W_groupSparse(1,:)),nOutputs); for s = 2:nVars fprintf('Number of tasks where variable %d was selected: %d (of %d)\n',s,nnz(W_groupSparse(s,:)),nOutputs); end fprintf('Total number of variables selected: %d (of %d)\n',nnz(sum(W_groupSparse(2:end,:),2)),nVars); pause
Computing Group-Sparse Multi-Task Classification Parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.63146e-04 6.92877e+02 2.25943e+01
2 3 16 1.00000e+00 6.01621e+02 4.46004e+00
3 4 28 1.00000e+00 6.00586e+02 3.56626e+00
4 5 40 1.00000e+00 6.00077e+02 1.99417e+00
5 6 52 1.00000e+00 5.99967e+02 6.37449e-01
6 7 64 1.00000e+00 5.99963e+02 1.96763e-01
7 8 75 1.00000e+00 5.99963e+02 5.62389e-02
8 9 87 1.00000e+00 5.99963e+02 2.11416e-02
9 10 97 1.00000e+00 5.99963e+02 3.10355e-03
10 11 104 1.00000e+00 5.99963e+02 8.99030e-04
11 12 111 1.00000e+00 5.99963e+02 1.33924e-04
Directional Derivative below progTol
Number of classes where bias variable was selected: 10 (of 10)
Number of tasks where variable 2 was selected: 10 (of 10)
Number of tasks where variable 3 was selected: 0 (of 10)
Number of tasks where variable 4 was selected: 10 (of 10)
Number of tasks where variable 5 was selected: 0 (of 10)
Number of tasks where variable 6 was selected: 0 (of 10)
Number of tasks where variable 7 was selected: 0 (of 10)
Number of tasks where variable 8 was selected: 0 (of 10)
Number of tasks where variable 9 was selected: 0 (of 10)
Number of tasks where variable 10 was selected: 0 (of 10)
Number of tasks where variable 11 was selected: 0 (of 10)
Number of tasks where variable 12 was selected: 0 (of 10)
Number of tasks where variable 13 was selected: 0 (of 10)
Number of tasks where variable 14 was selected: 0 (of 10)
Number of tasks where variable 15 was selected: 0 (of 10)
Number of tasks where variable 16 was selected: 0 (of 10)
Number of tasks where variable 17 was selected: 0 (of 10)
Number of tasks where variable 18 was selected: 0 (of 10)
Number of tasks where variable 19 was selected: 0 (of 10)
Number of tasks where variable 20 was selected: 0 (of 10)
Number of tasks where variable 21 was selected: 10 (of 10)
Number of tasks where variable 22 was selected: 10 (of 10)
Number of tasks where variable 23 was selected: 0 (of 10)
Number of tasks where variable 24 was selected: 0 (of 10)
Number of tasks where variable 25 was selected: 0 (of 10)
Total number of variables selected: 4 (of 25)
Low-Rank Multi-Task Classification
We will solve min_W nll(W,X,Y) s.t. |W|_sigma <= tau, where nll(W,X,Y) is the negative log-likelihood in a simultaneous binary logistic regression model, and where the nuclear norm |W|_sigma encourages W to be low-rank
W = zeros(nVars,nOutputs); funProj = @(w)traceProject(w,nVars,tau); fprintf('\nComputing Low-Rank Multi-Task Classification Parameters...\n'); W(:) = minConf_PQN(funObj,W(:),funProj); s = svd(W); fprintf('Number of non-zero singular values: %d (of %d)\n',sum(s > 1e-4),length(s)); pause
Computing Low-Rank Multi-Task Classification Parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.63146e-04 6.93116e+02 1.72961e-01
2 3 16 1.00000e+00 5.73676e+02 1.24511e-01
3 4 28 1.00000e+00 5.71969e+02 1.10654e-01
4 5 40 1.00000e+00 5.71629e+02 1.02558e-01
5 6 52 1.00000e+00 5.71608e+02 8.05868e-02
6 7 64 1.00000e+00 5.71608e+02 4.08470e-02
7 8 75 1.00000e+00 5.71608e+02 1.54377e-02
8 9 84 1.00000e+00 5.71608e+02 2.05653e-03
9 10 92 1.00000e+00 5.71608e+02 9.97128e-04
10 11 100 1.00000e+00 5.71608e+02 1.28489e-04
Directional Derivative below progTol
Number of non-zero singular values: 3 (of 10)
L_1,inf Blockwise-Sparse Graphical Lasso
We will solve nll(K,S) + sum_b lambda_b||K_b||_inf, where nll(K,S) is the Gaussian negative log-likelihood and the 'blocks' b encourage blockwise sparsity in the matrix between 'groups' g
We solve this non-differentiable problem by solving the convex dual problem: min_W -logdet(S + W), s.t. sum_b |W_b|_inf <= lambda
Using the L_1,inf mixed-norm to encourage blockwise sparsity, and the derivation of the convex dual problem are described in: Duchi, Gould, and Koller. Projected Subgradient Methods for Learning Sparse Gaussians. UAI (2008).
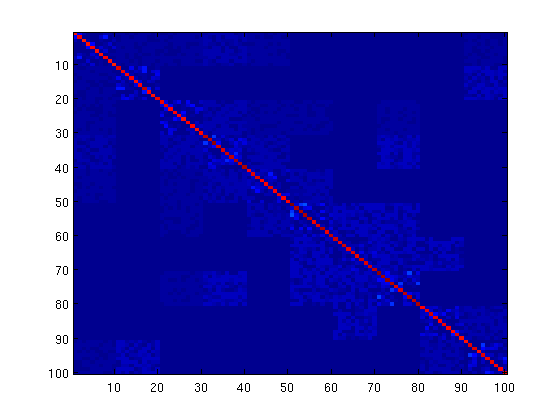
% Generate a set of variable groups nNodes = 100; nGroups = 10; groups = repmat(1:nNodes/nGroups,nGroups,1); groups = groups(:); % Generate a positive-definite matrix that is sparse within groups, and % blockwise sparse between groups betweenSparsity = (rand(nGroups) > .75).*triu(ones(nGroups),1); adj = triu(randn(nNodes).*(rand(nNodes) > .1),1); for g1 = 1:nGroups for g2 = g1+1:nGroups if betweenSparsity(g1,g2) == 0 adj(groups==g1,groups==g2) = 0; end end end adj = adj+adj'; tau = 1; invCov = adj + tau*eye(nNodes); while ~ispd(invCov) tau = tau*2; invCov = adj + tau*eye(nNodes); end mu = randn(nNodes,1); % Sample from the GGM nInstances = 500; C = inv(invCov); R = chol(C)'; X = zeros(nInstances,nNodes); for i = 1:nInstances X(i,:) = (mu + R*randn(nNodes,1))'; end % Center and Standardize X = standardizeCols(X); % Compute empirical covariance S = cov(X); % Set up Objective Function funObj = @(K)logdetFunction(K,S); % Set up Weights on penalty (multiply lambda by number of elements in % block) lambda = 10/nInstances; for g = 1:nGroups nBlockElements(g,1) = sum(groups==g); end lambdaBlock = setdiag(lambda * nBlockElements*nBlockElements',lambda); lambdaBlock = lambdaBlock(:); funProj = @(K)projectLinf1(K,nNodes,nBlockElements,lambdaBlock); % Initial guess of parameters W = lambda*eye(nNodes); % Solve with PQN fprintf('\nComputing L_1,inf Blockwise-Sparse Graphical Lasso Parameters...\n'); W(:) = minConf_PQN(funObj,W(:),funProj); K = inv(S+W); figure imagesc(abs(K)) pause
Computing L_1,inf Blockwise-Sparse Graphical Lasso Parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.33147e-03 1.54715e+01 3.07292e-01
2 3 16 1.00000e+00 7.30547e+00 9.08283e-02
3 4 28 1.00000e+00 4.41716e+00 3.31314e-02
4 5 40 1.00000e+00 3.95820e+00 2.07873e-02
5 6 52 1.00000e+00 3.88628e+00 8.89573e-03
6 7 64 1.00000e+00 3.87674e+00 3.58001e-03
7 8 76 1.00000e+00 3.87530e+00 1.98297e-03
8 9 88 1.00000e+00 3.87506e+00 5.66522e-04
9 10 100 1.00000e+00 3.87499e+00 3.09082e-04
10 11 112 1.00000e+00 3.87498e+00 4.65249e-04
11 12 124 1.00000e+00 3.87498e+00 7.38526e-05
12 13 135 1.00000e+00 3.87498e+00 5.38388e-05
13 14 147 1.00000e+00 3.87498e+00 3.69698e-05
14 15 159 1.00000e+00 3.87498e+00 3.32326e-05
15 16 165 1.00000e+00 3.87498e+00 4.06379e-06
First-Order Optimality Conditions Below optTol
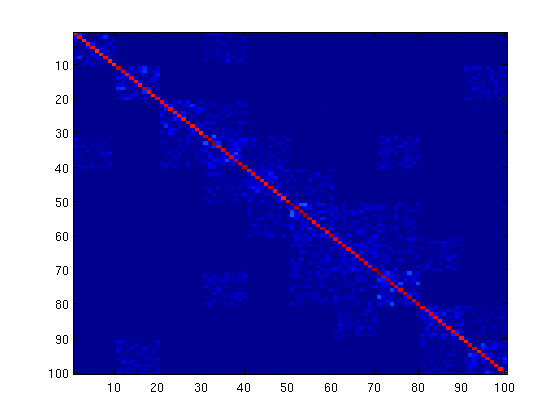
L_1,2 Blockwise-Sparse Graphical Lasso
Same as the above, but we use the L_1,2 group-norm instead of L_1,inf, as discussed in the PQN paper.
lambdaBlock = lambdaBlock/5; funProj = @(K)projectLinf2(K,nNodes,nBlockElements,lambdaBlock); % Initial guess of parameters W = lambda*eye(nNodes); % Solve with PQN fprintf('\nComputing L_1,2 Blockwise-Sparse Graphical Lasso Parameters...\n'); W(:) = minConf_PQN(funObj,W(:),funProj); K = inv(S+W); figure imagesc(abs(K)) pause
Computing L_1,2 Blockwise-Sparse Graphical Lasso Parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.26362e-03 1.77151e+01 1.58734e-01
2 3 16 1.00000e+00 9.52799e+00 9.38708e-02
3 4 28 1.00000e+00 5.75888e+00 5.11887e-02
4 5 40 1.00000e+00 5.04321e+00 2.54468e-02
5 6 52 1.00000e+00 4.90755e+00 1.72770e-02
6 7 64 1.00000e+00 4.88031e+00 8.38630e-03
7 8 76 1.00000e+00 4.87530e+00 4.83360e-03
8 9 88 1.00000e+00 4.87421e+00 2.13371e-03
9 10 100 1.00000e+00 4.87371e+00 7.76676e-04
10 11 112 1.00000e+00 4.87359e+00 2.33940e-03
11 12 124 1.00000e+00 4.87355e+00 4.84442e-04
12 13 136 1.00000e+00 4.87355e+00 1.76255e-04
13 14 148 1.00000e+00 4.87354e+00 6.12743e-05
14 15 160 1.00000e+00 4.87354e+00 1.02723e-04
15 16 172 1.00000e+00 4.87354e+00 4.31139e-05
16 17 183 1.00000e+00 4.87354e+00 1.02161e-05
17 18 191 1.00000e+00 4.87354e+00 7.88540e-06
First-Order Optimality Conditions Below optTol
Linear Regression with the Over-Lasso
We will solve the "Over-Lasso" problem: min_w |Xw-Y|^2 + lambda * sum_g |v_g|, s.t. sum v_i = w_i This is similar to the 'group' lasso' problems above, but in this case each variable is represented as a linear combination of 'sub' variables 'v', and these sub variables can belong to different groups. This leads to sparse solutions that tend to be unions of groups
We solve this problem by eliminating w, and using auxiliary variables to make the problem differentiable
The "Over-Lasso" regularizer and the method of eliminating w are described in: Jacob, Obozinski, and Vert. Group Lasso with Overlap and Graph Lasso. ICML (2009).
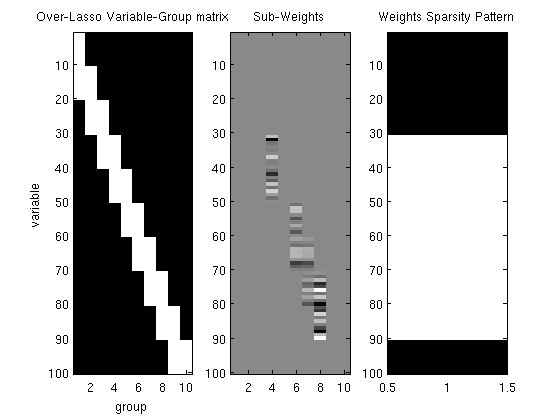
% Make variable-group membership matrix nVars = 100; nGroups = 10; varGroupMatrix = zeros(nVars,nGroups); offset = 0; for g = 1:nGroups varGroupMatrix(offset+1:min(offset+2*nVars/nGroups,nVars),g) = 1; offset = offset + nVars/nGroups; end % Generate synthetic data nInstances = 250; X = randn(nInstances,nVars); w = zeros(nVars,1); for g = 1:nGroups % Make some groups relevant if rand > .66 w(varGroupMatrix(:,g)==1) = randn(sum(varGroupMatrix(:,g)==1),1); end end y = X*w + randn(nInstances,1); % Initial guess of parameters vInd = find(varGroupMatrix==1); nSubVars = length(vInd); v = zeros(nSubVars,1); % Set up Objective Function lambda = 2000; alpha = zeros(nGroups,1); funObj = @(w)SquaredError(w,X,y); penalizedFunObj = @(vAlpha)overLassoLoss(vAlpha,varGroupMatrix,lambda,funObj); % Set up sub-variable groups subGroups = zeros(nSubVars,1); offset = 0; for g = 1:nGroups subGroupLength = sum(varGroupMatrix(:,g)); subGroups(offset+1:offset+subGroupLength) = g; offset = offset+subGroupLength; end % Set up L_1,2 Projection Function [groupStart,groupPtr] = groupl1_makeGroupPointers(subGroups); funProj = @(vAlpha)auxGroupL2Project(vAlpha,nSubVars,groupStart,groupPtr); % Solve with PQN fprintf('\nComputing over-lasso regularized linear regression parameters...\n'); vAlpha = minConf_PQN(penalizedFunObj,[v;alpha],funProj); % Extract parameters from augmented vector v = vAlpha(1:nSubVars); v(abs(v) < 1e-4) = 0; % Form sub-weight matrix vFull, and weight vector w vFull = zeros(nVars,nGroups); vFull(vInd) = v; w = sum(vFull,2); figure subplot(1,3,1); imagesc(varGroupMatrix); ylabel('variable'); xlabel('group'); title('Over-Lasso Variable-Group matrix'); subplot(1,3,2); imagesc(vFull);colormap gray title('Sub-Weights'); subplot(1,3,3); imagesc(w~=0); title('Weights Sparsity Pattern'); for g = 1:nGroups fprintf('Number of variables selected from group %d: %d (of %d)\n',g,nnz(w(varGroupMatrix(:,g)==1)),sum(varGroupMatrix(:,g))); end fprintf('\n'); for g = 1:nGroups-1 overlapInd = find(varGroupMatrix(:,g)==1 & varGroupMatrix(:,g+1)==1); fprintf('Number of variables selected from group %d-%d overlap: %d (of %d)\n',g,g+1,nnz(w(overlapInd)),length(overlapInd)); end pause
Computing over-lasso regularized linear regression parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 9.71256e-06 2.12660e+04 6.58767e+02
2 3 16 1.00000e+00 1.91252e+04 8.71746e+01
3 4 28 1.00000e+00 1.90613e+04 7.07454e+01
4 5 40 1.00000e+00 1.89302e+04 3.73046e+01
5 6 52 1.00000e+00 1.88984e+04 1.87517e+01
6 7 64 1.00000e+00 1.88807e+04 2.34453e+01
7 8 76 1.00000e+00 1.88772e+04 3.27563e+01
8 9 88 1.00000e+00 1.88728e+04 3.02722e+01
9 10 100 1.00000e+00 1.88643e+04 1.60727e+00
10 11 112 1.00000e+00 1.88621e+04 4.54495e+00
11 12 124 1.00000e+00 1.88608e+04 1.11958e+01
12 13 136 1.00000e+00 1.88602e+04 1.08807e+01
13 14 148 1.00000e+00 1.88593e+04 5.42940e+00
14 15 160 1.00000e+00 1.88591e+04 1.04790e+00
15 16 172 1.00000e+00 1.88591e+04 4.51838e-01
16 17 184 1.00000e+00 1.88591e+04 2.39230e-01
17 18 196 1.00000e+00 1.88591e+04 1.05892e-01
18 19 208 1.00000e+00 1.88591e+04 2.48399e-02
19 20 220 1.00000e+00 1.88591e+04 5.28073e-03
20 21 231 1.00000e+00 1.88591e+04 1.00800e-03
Directional Derivative below progTol
Number of variables selected from group 1: 0 (of 20)
Number of variables selected from group 2: 0 (of 20)
Number of variables selected from group 3: 10 (of 20)
Number of variables selected from group 4: 20 (of 20)
Number of variables selected from group 5: 20 (of 20)
Number of variables selected from group 6: 20 (of 20)
Number of variables selected from group 7: 20 (of 20)
Number of variables selected from group 8: 20 (of 20)
Number of variables selected from group 9: 10 (of 20)
Number of variables selected from group 10: 0 (of 10)
Number of variables selected from group 1-2 overlap: 0 (of 10)
Number of variables selected from group 2-3 overlap: 0 (of 10)
Number of variables selected from group 3-4 overlap: 10 (of 10)
Number of variables selected from group 4-5 overlap: 10 (of 10)
Number of variables selected from group 5-6 overlap: 10 (of 10)
Number of variables selected from group 6-7 overlap: 10 (of 10)
Number of variables selected from group 7-8 overlap: 10 (of 10)
Number of variables selected from group 8-9 overlap: 10 (of 10)
Number of variables selected from group 9-10 overlap: 0 (of 10)
Kernelized dual form of support vector machines
We solve the Wolfe-dual of the hard-margin kernel support vector machine training problem: min_alpha -sum_i alpha_i + (1/2)sum_i sum_j alpha_i alpha_j y_i y_j k(x_i,x_j), s.t. alpha_i >= 0, sum_i alpha_i y_i = 0
The dual form of support vector machine is described at: Dual Form of SVMs SVMs for Non-linear Classification
My implementation of the projection requires O(n^3). This could clearly be reduced to O(n^2), but I haven't yet worked out whether it can be done in O(n log n) or O(n).
% Generate synthetic data nInstances = 50; nVars = 100; nExamplePoints = 5; % Set to 1 for linear classifier, higher for more non-linear nClasses = 2; % examplePoints = randn(nClasses*nExamplePoints,nVars); % X = 2*rand(nInstances,nVars)-1; % y = zeros(nInstances,1); % for i = 1:nInstances % dists = sum((repmat(X(i,:),nClasses*nExamplePoints,1) - examplePoints).^2,2); % [minVal minInd] = min(dists); % y(i,1) = sign(mod(minInd,nClasses)-.5); % end X = randn(nInstances,nVars); w = randn(nVars,1); y = sign(X*w + randn(nInstances,1)); % Put positive instances first (used by projection) [y,sortedInd] = sort(y,'descend'); X = X(sortedInd,:); nPositive = min(find(y==-1)); % Compute Gram matrix rbfScale = 1; K = kernelLinear(X,X); % Initial guess of parameters alpha = rand(nInstances,1); % Set up objective function funObj = @(alpha)dualSVMLoss(alpha,K,y); % Set up projection %(projection function assumes that positive instances come first) funProj = @(alpha)dualSVMproject(alpha,nPositive); % Solve with PQN fprintf('\nCompute dual SVM parameters...\n'); alpha = minConf_PQN(funObj,alpha,funProj); fprintf('Number of support vectors: %d\n',sum(alpha > 1e-4)); pause
Compute dual SVM parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 2.45883e-04 1.25825e+03 4.41319e+01
2 3 16 1.00000e+00 5.48524e+01 1.81122e+01
3 4 28 1.00000e+00 1.64114e+01 1.03732e+00
4 5 40 1.00000e+00 2.22151e+00 4.96778e+00
5 6 52 1.00000e+00 -5.11628e-03 1.85774e+00
6 7 63 1.00000e+00 -2.15324e-01 1.26787e+00
7 8 74 1.00000e+00 -2.54407e-01 4.74583e-01
8 9 85 1.00000e+00 -2.71839e-01 3.59047e-01
9 10 96 1.00000e+00 -2.77304e-01 1.29107e-01
10 11 107 1.00000e+00 -2.79554e-01 1.51559e-01
11 12 118 1.00000e+00 -2.80615e-01 8.36431e-02
12 13 129 1.00000e+00 -2.81132e-01 2.56156e-02
13 14 140 1.00000e+00 -2.81236e-01 2.76263e-02
14 15 151 1.00000e+00 -2.81275e-01 1.33857e-02
15 16 162 1.00000e+00 -2.81287e-01 8.15209e-03
16 17 173 1.00000e+00 -2.81293e-01 1.07857e-02
17 18 184 1.00000e+00 -2.81295e-01 5.03575e-03
18 19 195 1.00000e+00 -2.81296e-01 2.38382e-03
19 20 204 1.00000e+00 -2.81296e-01 1.50424e-03
20 21 215 1.00000e+00 -2.81296e-01 8.33735e-04
21 22 226 1.00000e+00 -2.81296e-01 1.01088e-03
22 23 232 1.00000e+00 -2.81296e-01 4.14650e-04
23 24 238 1.00000e+00 -2.81296e-01 1.57150e-04
24 25 245 1.00000e+00 -2.81296e-01 1.08646e-04
25 26 251 1.00000e+00 -2.81296e-01 6.25657e-05
Function value changing by less than progTol
Number of support vectors: 41
Smooth (Primal) Support Vector Machine with Multiple Kernel Learning
We will solve min_w hinge(w,X,y).^2, s.t. sum_k |w_k|_2 <= tau, where X contains the expansions of multiple kernels and we want to encourage selection of a sparse set of kernels.
By squaring the slack variables we get a once differentiable objective
The smooth support vector machine is described in: Lee and Mangasarian. SSVM: A Smooth Support Vector Machine. Computational Optimization and Applications (2001).
Using group-sparsity for multiple kernel learning is described in: Bach, Lanckriet, and Jordan. Multiple Kernel Learning, Conic Duality, and the SMO Algorithm. NIPS (2004).
nInstances = 1000; nKernels = 25; kernelSize = ceil(10*rand(nKernels,1)); X = zeros(nInstances,0); for k = 1:nKernels Xk = randn(nInstances,kernelSize(k)); % Add kernel to X = [X Xk]; end w = zeros(0,1); for k = 1:nKernels if rand > .9 % Only make ~10% of kernels are relevant w = [w;randn(kernelSize(k),1)]; else w = [w;zeros(kernelSize(k),1)]; end end y = sign(X*w + randn(nInstances,1)); % Initial guess of parameters wMKL = zeros(sum(kernelSize),1); % Set up objective function funObj = @(w)SSVMLoss(w,X,y); % Set up groups offset = 0; groups = zeros(size(w)); for k = 1:nKernels groups(offset+1:offset+kernelSize(k),1) = k; offset = offset+kernelSize(k); end % Set up L_1,2 Projection Function tau = 1; funProj = @(w)groupL2Proj(w,tau,groups); % Solve with PQN fprintf('\nComputing parameters of smooth SVM with multiple kernels...\n'); wMKL = minConf_PQN(funObj,wMKL,funProj); wMKL(abs(wMKL) < 1e-4) = 0; wMKL' fprintf('Number of kernels selected: %d (of %d)\n',sum(accumarray(groups,abs(wMKL)) > 1e-4),nKernels); pause
Computing parameters of smooth SVM with multiple kernels...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 9.40461e-05 9.99863e+02 5.18399e-01
2 3 16 1.00000e+00 4.42999e+02 2.47627e-01
3 4 28 1.00000e+00 4.28820e+02 1.83484e-01
4 5 39 1.00000e+00 4.23080e+02 8.70814e-02
5 6 49 1.00000e+00 4.22682e+02 6.22413e-01
6 7 60 1.00000e+00 4.22668e+02 1.37036e-01
7 8 72 1.00000e+00 4.22667e+02 1.28652e-02
8 9 80 1.00000e+00 4.22667e+02 1.01382e-02
9 10 89 1.00000e+00 4.22667e+02 1.15509e-03
10 11 95 1.00000e+00 4.22667e+02 1.60054e-04
Directional Derivative below progTol
ans =
Columns 1 through 7
0 0 0 0 0 0 0
Columns 8 through 14
0 -0.0051 0.0093 0.0035 -0.0063 -0.0044 0.0051
Columns 15 through 21
-0.0023 0 0 0 0 0 0
Columns 22 through 28
0 0 0 0 0 0 0
Columns 29 through 35
0 0 0 0 0 0 0
Columns 36 through 42
0 0 0 0 0 0 0
Columns 43 through 49
0 0 0 0 0 0 0
Columns 50 through 56
0 0 0 0 0 0 0
Columns 57 through 63
0 0 0 0 0 0 0
Columns 64 through 70
0 0 0 0 0 0 0
Columns 71 through 77
0 0 0 -0.0052 -0.0109 -0.0063 0.0124
Columns 78 through 84
-0.0019 -0.0071 -0.0113 0 0 0 0
Columns 85 through 91
0 0 0 0 0 0 0
Columns 92 through 98
0 0 0 0 0 0 0
Columns 99 through 105
0 0 -0.0006 -0.0003 0.0001 -0.0009 0.0002
Columns 106 through 112
0 0.0003 0 0 -0.0200 -0.0295 -0.0002
Columns 113 through 119
-0.0031 -0.0066 -0.0011 -0.0056 0.0031 0.3783 0.2411
Columns 120 through 126
-0.4558 0.2762 0.1578 0.0720 -0.0872 0.1969 -0.1967
Columns 127 through 133
0.3914 -0.0002 0.0003 0.0002 0 -0.0003 -0.0002
Columns 134 through 140
0 0.0003 -0.0001 0.0001 -0.0024 0.0020 -0.0006
Columns 141 through 145
0.0244 -0.0361 0.0280 -0.0198 0
Number of kernels selected: 7 (of 25)
Conditional Random Field Feature Selection
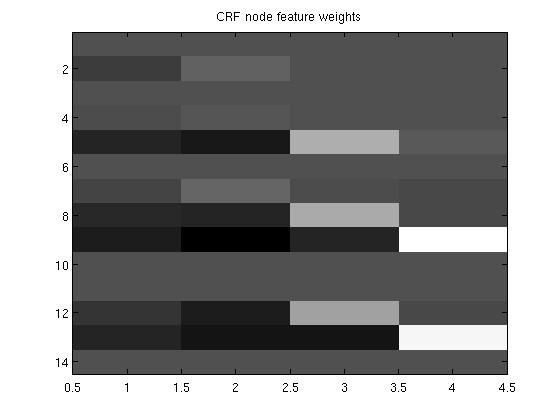
We will solve min_{w,v} nll(w,v,x,y) + lambda * sum_f |w_f|_2, where nll(w,v,x,y) is the negative log-likelihood for a log-linear chain-structured conditional random field and each 'group' f is the set of parameters associated with a single input feature, leading to sparsity in the terms of the input features
load wordData.mat lambda = 20; % Initialize [w,vs,ve,v] = crfChain_initWeights(nFeatures,nStates); featureStart = cumsum([1 nFeatures(1:end)]); % data structure which relates high-level 'features' to elements of w sentences = crfChain_initSentences(y); nSentences = size(sentences,1); maxSentenceLength = 1+max(sentences(:,2)-sentences(:,1)); wv = [w(:);vs;ve;v(:)]; nVars = length(wv); funObj = @(wv)crfChain_loss(wv,X,y,nStates,nFeatures,featureStart,sentences); % Put all node variables associated with individual features into groups groups_w = repmat([1:sum(nFeatures)]',[1 nStates]); % Don't penalize edge variables groups_vs= zeros(size(vs)); groups_ve= zeros(size(ve)); groups_v= zeros(size(v)); groups = [groups_w(:);groups_vs;groups_ve;groups_v(:)]; nGroups = max(groups); % Initialize auxiliary variables alpha = zeros(nGroups,1); penalizedFunObj = @(w)auxGroupLoss(w,groups,lambda,funObj); % Set up L_1,2 Projection Function [groupStart,groupPtr] = groupl1_makeGroupPointers(groups); funProj = @(w)auxGroupL2Project(w,nVars,groupStart,groupPtr); % Solve with PQN fprintf('\nComputing feature-sparse conditional random field parameters...\n'); wva = minConf_PQN(penalizedFunObj,[wv;alpha],funProj); [w,vs,ve,v] = crfChain_splitWeights(wva(1:nVars),featureStart,nStates); figure imagesc(w);colormap gray title('CRF node feature weights'); pause
Computing feature-sparse conditional random field parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 4.13907e-04 1.16766e+03 6.31389e+01
2 3 16 1.00000e+00 8.79023e+02 5.35717e+01
3 4 28 1.00000e+00 8.39557e+02 2.54508e+01
4 5 40 1.00000e+00 8.20969e+02 1.41169e+01
5 6 51 1.00000e+00 7.96231e+02 1.32832e+01
6 7 63 1.00000e+00 7.78225e+02 6.46104e+00
7 8 75 1.00000e+00 7.72086e+02 3.19869e+00
8 9 87 1.00000e+00 7.67519e+02 1.11609e+01
9 10 99 1.00000e+00 7.64916e+02 5.39515e+00
10 11 111 1.00000e+00 7.61398e+02 5.54300e+00
11 12 123 1.00000e+00 7.59558e+02 4.14841e+00
12 13 135 1.00000e+00 7.58421e+02 1.17329e+00
13 14 147 1.00000e+00 7.58089e+02 2.69375e+00
14 15 158 1.00000e+00 7.57927e+02 2.16008e+00
15 16 170 1.00000e+00 7.57711e+02 8.79680e-01
16 17 182 1.00000e+00 7.57668e+02 4.16621e-01
17 18 194 1.00000e+00 7.57648e+02 2.19777e-01
18 19 206 1.00000e+00 7.57641e+02 1.48976e-01
19 20 218 1.00000e+00 7.57639e+02 1.41745e-01
20 21 230 1.00000e+00 7.57637e+02 1.02384e-01
21 22 242 1.00000e+00 7.57636e+02 5.13171e-02
22 23 253 1.00000e+00 7.57636e+02 3.34465e-02
23 24 265 1.00000e+00 7.57636e+02 1.65591e-02
24 25 277 1.00000e+00 7.57636e+02 1.18514e-02
25 26 289 1.00000e+00 7.57636e+02 7.18780e-03
26 27 301 1.00000e+00 7.57636e+02 4.87103e-03
27 28 313 1.00000e+00 7.57636e+02 3.04077e-03
28 29 325 1.00000e+00 7.57636e+02 2.40636e-03
29 30 337 1.00000e+00 7.57636e+02 1.00814e-03
30 31 348 1.00000e+00 7.57636e+02 5.67028e-04
31 32 360 1.00000e+00 7.57636e+02 5.51060e-04
32 33 370 1.00000e+00 7.57636e+02 3.93047e-04
33 34 381 1.00000e+00 7.57636e+02 2.28419e-04
34 35 393 1.00000e+00 7.57636e+02 1.40384e-04
35 36 398 1.00000e+00 7.57636e+02 1.49688e-04
Function value changing by less than progTol
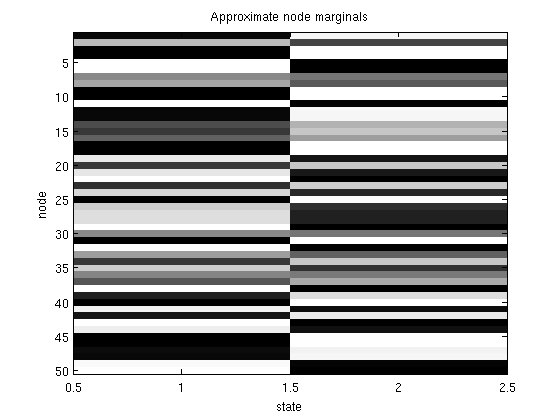
Approximating node marginals in undirected graphical models with variational mean field
We want to approximate marginals in a pairwise Markov random field by minimizing the Gibbs free energy under a mean-field (factorized) approximation.
Variational approximations and the mean field free energy are described in: Yedidia, Freeman, Weiss. Understanding Belief Propagation and Its Generalizations. IJCAI (2001).
The projection reduces to a series of independent projections on the simplex.
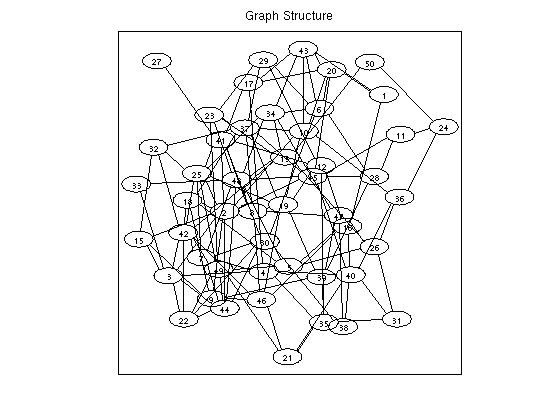
% Generate potentials a pairiwse graphical model nNodes = 50; nStates = 2; adj = zeros(nNodes); for n1 = 1:nNodes for n2 = n1+1:nNodes if rand > .9 adj(n1,n2) = 1; adj(n2,n1) = 1; end end end edgeStruct = UGM_makeEdgeStruct(adj,nStates); nEdges = edgeStruct.nEdges; edgeEnds = edgeStruct.edgeEnds; nodePot = rand(nNodes,nStates); edgePot = rand(nStates,nStates,nEdges); % Intialize marginals nodeBel = (1/nStates)*ones(nNodes,nStates); % Make objective function funObj = @(nodeBel)MeanFieldGibbsFreeEnergyLoss(nodeBel,nodePot,edgePot,edgeEnds); % Make projection function funProj = @(nodeBel)MeanFieldGibbsFreeEnergyProject(nodeBel,nNodes,nStates); % Solve with PQN fprintf('\nMinimizing Mean Field Gibbs Free Energy of pairwise undirected graphical model...\n'); nodeBel(:) = minConf_PQN(funObj,nodeBel(:),funProj); figure imagesc(nodeBel);colormap gray title('Approximate node marginals'); ylabel('node'); xlabel('state'); figure drawGraph(adj); title('Graph Structure'); pause
Minimizing Mean Field Gibbs Free Energy of pairwise undirected graphical model...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 1.44167e-03 1.62658e+02 4.99279e-01
2 3 16 1.00000e+00 1.31962e+02 8.52303e-01
3 4 28 1.00000e+00 1.30132e+02 7.80049e-01
4 5 40 1.00000e+00 1.27262e+02 4.72673e-01
5 6 52 1.00000e+00 1.26291e+02 4.18405e-01
6 7 64 1.00000e+00 1.26151e+02 4.03896e-01
7 8 76 1.00000e+00 1.25875e+02 9.99358e-01
8 9 88 1.00000e+00 1.25780e+02 3.45929e-01
9 10 99 1.00000e+00 1.25711e+02 3.52333e-01
10 11 109 1.00000e+00 1.25578e+02 3.97842e-01
11 12 120 1.00000e+00 1.25422e+02 5.79143e-01
12 13 131 1.00000e+00 1.25320e+02 2.18241e-01
13 14 142 1.00000e+00 1.25227e+02 2.20488e-01
14 15 153 1.00000e+00 1.25136e+02 2.40032e-01
15 16 164 1.00000e+00 1.25029e+02 2.13415e-01
16 17 175 1.00000e+00 1.24977e+02 1.80182e-01
17 18 186 1.00000e+00 1.24944e+02 3.82755e-01
18 19 198 1.00000e+00 1.24935e+02 3.28613e-01
19 20 210 1.00000e+00 1.24927e+02 1.29281e-01
20 21 221 1.00000e+00 1.24919e+02 1.89010e-01
21 22 233 1.00000e+00 1.24916e+02 5.97267e-02
22 23 245 1.00000e+00 1.24914e+02 4.86406e-02
23 24 256 1.00000e+00 1.24912e+02 3.25016e-02
24 25 267 1.00000e+00 1.24911e+02 2.93020e-02
25 26 278 1.00000e+00 1.24911e+02 2.23381e-02
26 27 289 1.00000e+00 1.24910e+02 2.25549e-02
27 28 301 1.00000e+00 1.24910e+02 1.32620e-02
28 29 313 1.00000e+00 1.24910e+02 1.36705e-02
29 30 325 1.00000e+00 1.24910e+02 9.27483e-03
30 31 337 1.00000e+00 1.24910e+02 5.73696e-03
31 32 349 1.00000e+00 1.24910e+02 3.15075e-03
32 33 360 1.00000e+00 1.24910e+02 3.61176e-03
33 34 372 1.00000e+00 1.24910e+02 2.62249e-03
34 35 383 1.00000e+00 1.24910e+02 1.14729e-03
35 36 395 1.00000e+00 1.24910e+02 1.92095e-03
36 37 406 1.00000e+00 1.24910e+02 1.02304e-03
37 38 418 1.00000e+00 1.24910e+02 7.10496e-04
38 39 429 1.00000e+00 1.24910e+02 4.60186e-04
39 40 441 1.00000e+00 1.24910e+02 2.55750e-04
40 41 452 1.00000e+00 1.24910e+02 1.81987e-04
41 42 463 1.00000e+00 1.24910e+02 1.66579e-04
42 43 474 1.00000e+00 1.24910e+02 3.50226e-04
43 44 484 1.00000e+00 1.24910e+02 1.58874e-04
44 45 496 1.00000e+00 1.24910e+02 3.99517e-05
Directional Derivative below progTol
neato - Graphviz version 2.20.2 (Tue Mar 2 19:03:41 UTC 2010)
Multi-State Markov Random Field Structure Learning
We will solve min_{w,v} nll(w,v,y), s.t. sum_e |v_e|_2 <= tau, where nll(w,v,y) is the negative log-likelihood for a log-linear Markov random field and each 'group' e is the set of parameters associated with an edge, leading to sparsity in the graph
Using group-sparsity to select edges in a multi-state Markov random field is discussed in: Schmidt, Murphy, Fung, and Rosales. Structure Learning in Random Field for Heart Motion Abnormality Detection. CVPR (2008).
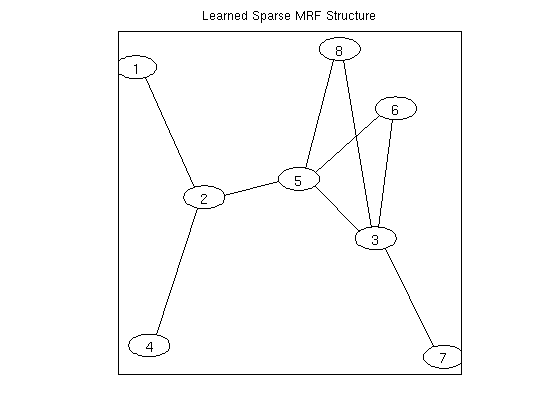
% Generate Data nInstances = 250; nNodes = 8; edgeDensity = .33; nStates = 3; ising = 0; tied = 0; useMex = 1; y = UGM_generate(nInstances,0,nNodes,edgeDensity,nStates,ising,tied); % Set up MRF adj = fullAdjMatrix(nNodes); edgeStruct = UGM_makeEdgeStruct(adj,nStates,useMex); [nodeMap,edgeMap] = UGM_makeMRFmaps(edgeStruct,ising,tied); % Initialize Variables nNodeParams = max(nodeMap(:)); nParams = max(edgeMap(:)); nEdgeParams = nParams-nNodeParams; w = zeros(nParams,1); % Make Groups groups = zeros(nParams,1); for e = 1:edgeStruct.nEdges edgeParams = edgeMap(:,:,e,:); groups(edgeParams(:)) = e; end % Set up Objective Function suffStat = UGM_MRF_computeSuffStat(y,nodeMap,edgeMap,edgeStruct); funObj = @(w)UGM_MRF_NLL(w,nInstances,suffStat,nodeMap,edgeMap,edgeStruct,@UGM_Infer_Exact); lambdaL2 = 1; penalizedFunObj = @(w)penalizedL2(w,funObj,lambdaL2); % Set up L_1,2 Projection Function tau = 5; funProj = @(w)groupL2Proj(w,tau,groups); % Solve with PQN fprintf('\nComputing Sparse Markov random field parameters...\n'); w = minConf_PQN(penalizedFunObj,w,funProj); w(abs(w) < 1e-4) = 0; % Check selected variables for e = 1:edgeStruct.nEdges params = edgeMap(:,:,e); params = params(params(:)~=0); fprintf('Number of non-zero variables associated with edge from %d to %d: %d (of %d)\n',edgeStruct.edgeEnds(e,1),edgeStruct.edgeEnds(e,2),nnz(w(params)),numel(w(params))); end % Make final adjacency matrix adj = zeros(nNodes); for e = 1:edgeStruct.nEdges params = edgeMap(:,:,e); params = params(params(:)~=0); if any(w(params)~=0) n1 = edgeStruct.edgeEnds(e,1); n2 = edgeStruct.edgeEnds(e,2); adj(n1,n2) = 1; adj(n2,n1) = 1; end end figure drawGraph(adj); title('Learned Sparse MRF Structure'); pause
Exact Sampling
Computing Sparse Markov random field parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 8.65202e-05 2.18482e+03 1.61649e+02
2 3 16 1.00000e+00 8.58677e+02 1.98063e+01
3 4 28 1.00000e+00 8.39193e+02 1.27737e+01
4 5 40 1.00000e+00 8.27884e+02 9.19846e+00
5 6 52 1.00000e+00 8.11888e+02 4.33189e+00
6 7 63 1.00000e+00 8.11244e+02 2.39436e+01
7 8 75 1.00000e+00 8.05800e+02 6.99203e+00
8 9 87 1.00000e+00 8.04591e+02 3.73055e+00
9 10 99 1.00000e+00 8.03432e+02 4.10645e+00
10 11 111 1.00000e+00 8.02194e+02 4.28152e+00
11 12 123 1.00000e+00 8.01689e+02 7.51540e+00
12 13 135 1.00000e+00 8.01154e+02 3.91117e+00
13 14 147 1.00000e+00 8.00701e+02 3.32273e+00
14 15 158 1.00000e+00 8.00312e+02 2.69325e+00
15 16 168 1.00000e+00 7.99896e+02 2.15604e+00
16 17 179 1.00000e+00 7.99403e+02 2.38568e+00
17 18 190 1.00000e+00 7.98913e+02 2.16397e+00
18 19 201 1.00000e+00 7.98279e+02 1.17471e+00
19 20 212 1.00000e+00 7.97936e+02 7.70176e-01
20 21 224 1.00000e+00 7.97840e+02 7.30143e-01
21 22 235 1.00000e+00 7.97762e+02 7.60268e-01
22 23 246 1.00000e+00 7.97702e+02 5.70059e-01
23 24 257 1.00000e+00 7.97658e+02 1.41639e+00
24 25 269 1.00000e+00 7.97633e+02 5.35854e-01
25 26 281 1.00000e+00 7.97622e+02 4.00744e-01
26 27 292 1.00000e+00 7.97608e+02 3.74958e-01
27 28 303 1.00000e+00 7.97593e+02 3.44633e-01
28 29 314 1.00000e+00 7.97571e+02 2.65858e-01
29 30 325 1.00000e+00 7.97554e+02 2.33143e-01
30 31 336 1.00000e+00 7.97532e+02 1.99139e-01
31 32 348 1.00000e+00 7.97528e+02 1.45973e-01
32 33 359 1.00000e+00 7.97525e+02 1.30455e-01
33 34 370 1.00000e+00 7.97523e+02 7.77846e-02
34 35 381 1.00000e+00 7.97522e+02 1.20532e-01
35 36 392 1.00000e+00 7.97522e+02 1.04226e-01
36 37 403 1.00000e+00 7.97521e+02 4.47146e-02
37 38 414 1.00000e+00 7.97521e+02 4.32276e-02
38 39 425 1.00000e+00 7.97520e+02 3.88135e-02
39 40 436 1.00000e+00 7.97520e+02 3.51474e-02
40 41 447 1.00000e+00 7.97520e+02 2.60144e-02
41 42 459 1.00000e+00 7.97520e+02 3.59869e-02
42 43 471 1.00000e+00 7.97520e+02 2.77704e-02
43 44 481 1.00000e+00 7.97520e+02 1.61027e-02
44 45 493 1.00000e+00 7.97519e+02 1.43819e-02
45 46 504 1.00000e+00 7.97519e+02 1.31595e-02
46 47 515 1.00000e+00 7.97519e+02 1.10195e-02
47 48 527 1.00000e+00 7.97519e+02 8.98387e-03
48 49 538 1.00000e+00 7.97519e+02 5.68701e-03
49 50 550 1.00000e+00 7.97519e+02 5.86993e-03
50 51 562 1.00000e+00 7.97519e+02 4.57134e-03
51 52 574 1.00000e+00 7.97519e+02 2.45114e-03
52 53 586 1.00000e+00 7.97519e+02 1.90106e-03
53 54 598 1.00000e+00 7.97519e+02 2.00244e-03
54 55 610 1.00000e+00 7.97519e+02 1.07678e-03
55 56 622 1.00000e+00 7.97519e+02 6.61842e-04
56 57 634 1.00000e+00 7.97519e+02 7.38063e-04
57 58 646 1.00000e+00 7.97519e+02 7.70531e-04
58 59 657 1.00000e+00 7.97519e+02 5.81262e-04
59 60 668 1.00000e+00 7.97519e+02 4.27253e-04
60 61 680 1.00000e+00 7.97519e+02 9.88395e-04
61 62 692 1.00000e+00 7.97519e+02 5.59799e-04
62 63 703 1.00000e+00 7.97519e+02 4.07185e-04
63 64 714 1.00000e+00 7.97519e+02 3.34542e-04
64 65 725 1.00000e+00 7.97519e+02 3.45916e-04
65 66 736 1.00000e+00 7.97519e+02 2.90131e-04
66 67 747 1.00000e+00 7.97519e+02 2.41294e-04
67 68 758 1.00000e+00 7.97519e+02 1.68164e-04
68 69 769 1.00000e+00 7.97519e+02 1.21657e-04
69 70 776 1.00000e+00 7.97519e+02 1.26649e-04
Directional Derivative below progTol
Number of non-zero variables associated with edge from 1 to 2: 9 (of 9)
Number of non-zero variables associated with edge from 1 to 3: 0 (of 9)
Number of non-zero variables associated with edge from 1 to 4: 0 (of 9)
Number of non-zero variables associated with edge from 1 to 5: 0 (of 9)
Number of non-zero variables associated with edge from 1 to 6: 0 (of 9)
Number of non-zero variables associated with edge from 1 to 7: 0 (of 9)
Number of non-zero variables associated with edge from 1 to 8: 0 (of 9)
Number of non-zero variables associated with edge from 2 to 3: 0 (of 9)
Number of non-zero variables associated with edge from 2 to 4: 9 (of 9)
Number of non-zero variables associated with edge from 2 to 5: 9 (of 9)
Number of non-zero variables associated with edge from 2 to 6: 0 (of 9)
Number of non-zero variables associated with edge from 2 to 7: 0 (of 9)
Number of non-zero variables associated with edge from 2 to 8: 0 (of 9)
Number of non-zero variables associated with edge from 3 to 4: 0 (of 9)
Number of non-zero variables associated with edge from 3 to 5: 9 (of 9)
Number of non-zero variables associated with edge from 3 to 6: 9 (of 9)
Number of non-zero variables associated with edge from 3 to 7: 9 (of 9)
Number of non-zero variables associated with edge from 3 to 8: 9 (of 9)
Number of non-zero variables associated with edge from 4 to 5: 0 (of 9)
Number of non-zero variables associated with edge from 4 to 6: 0 (of 9)
Number of non-zero variables associated with edge from 4 to 7: 0 (of 9)
Number of non-zero variables associated with edge from 4 to 8: 0 (of 9)
Number of non-zero variables associated with edge from 5 to 6: 9 (of 9)
Number of non-zero variables associated with edge from 5 to 7: 0 (of 9)
Number of non-zero variables associated with edge from 5 to 8: 9 (of 9)
Number of non-zero variables associated with edge from 6 to 7: 0 (of 9)
Number of non-zero variables associated with edge from 6 to 8: 0 (of 9)
Number of non-zero variables associated with edge from 7 to 8: 0 (of 9)
neato - Graphviz version 2.20.2 (Tue Mar 2 19:03:41 UTC 2010)
Conditional Random Field Structure Learning with Pseudo-Likelihood
We will solve min_{w,v} nll(w,v,x,y) + lambda * sum_e |v_e|_inf, where nll(w,v,x,y) is the negative log-likelihood for a log-linear conditional random field and each 'group' e is the set of parameters associated with an edge, leading to sparsity in the graph
To solve the problem, we use a pseudo-likelihood approximation of the negative log-likelihood, and convert the non-differentiable problem to a differentiable one by introducing auxiliary variables
Using group-sparsity to select edges in a conditional random field trained with pseudo-likelihood is discussed in: Schmidt, Murphy, Fung, and Rosales. Structure Learning in Random Field for Heart Motion Abnormality Detection. CVPR (2008).
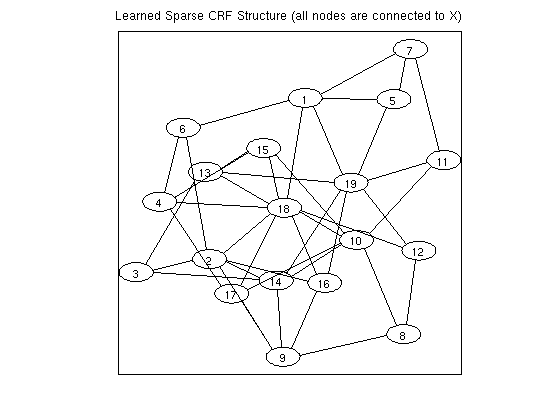
% Generate Data nInstances = 250; nFeatures = 10; nNodes = 20; edgeDensity = .25; nStates = 2; ising = 0; tied = 0; useMex = 1; [y,adj,X] = UGM_generate(nInstances,nFeatures,nNodes,edgeDensity,nStates,ising,tied); % Set up CRF adj = fullAdjMatrix(nNodes); edgeStruct = UGM_makeEdgeStruct(adj,nStates,useMex); % Make edge features Xedge = UGM_makeEdgeFeatures(X,edgeStruct.edgeEnds); [nodeMap,edgeMap] = UGM_makeCRFmaps(X,Xedge,edgeStruct,ising,tied); % Initialize Variables nNodeParams = max(nodeMap(:)); nVars = max(edgeMap(:)); w = zeros(nVars,1); % Make Groups groups = zeros(nVars,1); for e = 1:edgeStruct.nEdges edgeParams = edgeMap(:,:,e,:); groups(edgeParams(:)) = e; end nGroups = edgeStruct.nEdges; % Set up Objective Function funObj = @(w)UGM_CRF_PseudoNLL(w,X,Xedge,y,nodeMap,edgeMap,edgeStruct); lambdaL2 = 1; penalizedFunObj = @(w)penalizedL2(w,funObj,lambdaL2); % Initialize auxiliary variables that will bound norm lambda = 500; alpha = zeros(nGroups,1); auxFunObj = @(wAlpha)auxGroupLoss(wAlpha,groups,lambda,penalizedFunObj); % Set up L_1,inf Projection Function [groupStart,groupPtr] = groupl1_makeGroupPointers(groups); funProj = @(wAlpha)auxGroupLinfProject(wAlpha,nVars,groupStart,groupPtr); % Solve with PQN fprintf('\nComputing Sparse conditional random field parameters...\n'); wAlpha = minConf_PQN(auxFunObj,[w;alpha],funProj); w = wAlpha(1:nVars); w(abs(w) < 1e-4) = 0; % Check selected variables for e = 1:edgeStruct.nEdges params = edgeMap(:,:,e,:); params = params(params(:)~=0); fprintf('Number of non-zero variables associated with edge from %d to %d: %d (of %d)\n',edgeStruct.edgeEnds(e,1),edgeStruct.edgeEnds(e,2),nnz(w(params)),numel(w(params))); end % Make final adjacency matrix adj = zeros(nNodes); for e = 1:edgeStruct.nEdges params = edgeMap(:,:,e,:); params = params(params(:)~=0); if any(w(params)~=0) n1 = edgeStruct.edgeEnds(e,1); n2 = edgeStruct.edgeEnds(e,2); adj(n1,n2) = 1; adj(n2,n1) = 1; end end figure drawGraph(adj); title('Learned Sparse CRF Structure (all nodes are connected to X)');
Gibbs Sampling
Computing Sparse conditional random field parameters...
Iteration FunEvals Projections Step Length Function Val Opt Cond
1 2 4 3.52789e-06 3.46298e+03 6.37126e+01
2 3 16 1.00000e+00 2.96765e+03 3.31060e+01
3 4 28 1.00000e+00 2.88935e+03 2.62199e+01
4 5 39 1.00000e+00 2.76144e+03 1.65791e+01
5 6 50 1.00000e+00 2.65383e+03 1.21515e+01
6 7 61 1.00000e+00 2.56483e+03 1.07178e+01
7 8 73 1.00000e+00 2.51620e+03 8.46672e+00
8 9 85 1.00000e+00 2.48459e+03 5.90253e+00
9 10 97 1.00000e+00 2.46736e+03 4.42851e+00
10 11 109 1.00000e+00 2.45945e+03 3.27385e+00
11 12 121 1.00000e+00 2.45521e+03 2.24937e+00
12 13 133 1.00000e+00 2.45361e+03 1.65477e+00
13 14 145 1.00000e+00 2.45242e+03 1.17876e+00
14 15 157 1.00000e+00 2.45191e+03 9.55383e-01
15 16 169 1.00000e+00 2.45156e+03 6.70175e-01
16 17 181 1.00000e+00 2.45138e+03 5.36553e-01
17 18 193 1.00000e+00 2.45128e+03 4.16853e-01
18 19 205 1.00000e+00 2.45123e+03 3.04263e-01
19 20 217 1.00000e+00 2.45120e+03 2.06939e-01
20 21 229 1.00000e+00 2.45119e+03 1.39867e-01
21 22 241 1.00000e+00 2.45118e+03 1.03235e-01
22 23 253 1.00000e+00 2.45117e+03 7.68651e-02
23 24 265 1.00000e+00 2.45117e+03 5.60913e-02
24 25 277 1.00000e+00 2.45117e+03 4.48514e-02
25 26 289 1.00000e+00 2.45117e+03 4.21212e-02
26 27 301 1.00000e+00 2.45116e+03 2.97279e-02
27 28 313 1.00000e+00 2.45116e+03 3.80838e-02
28 29 324 1.00000e+00 2.45116e+03 4.14760e-02
29 30 335 1.00000e+00 2.45116e+03 4.08802e-02
30 31 347 1.00000e+00 2.45116e+03 2.81035e-02
31 32 358 1.00000e+00 2.45116e+03 3.07415e-02
32 33 369 1.00000e+00 2.45116e+03 3.11472e-02
33 34 380 1.00000e+00 2.45116e+03 3.06254e-02
34 35 391 1.00000e+00 2.45116e+03 3.77315e-02
35 36 403 1.00000e+00 2.45116e+03 4.23843e-02
36 37 415 1.00000e+00 2.45116e+03 3.87756e-02
37 38 427 1.00000e+00 2.45116e+03 3.13473e-02
38 39 438 1.00000e+00 2.45116e+03 2.59070e-02
39 40 450 1.00000e+00 2.45116e+03 2.61268e-02
40 41 462 1.00000e+00 2.45116e+03 2.27940e-02
41 42 474 1.00000e+00 2.45116e+03 1.81264e-02
42 43 485 1.00000e+00 2.45116e+03 1.52857e-02
43 44 496 1.00000e+00 2.45116e+03 1.76452e-02
44 45 508 1.00000e+00 2.45116e+03 2.07862e-02
45 46 518 1.00000e+00 2.45116e+03 1.75046e-02
46 47 529 1.00000e+00 2.45116e+03 1.41643e-02
47 48 540 1.00000e+00 2.45116e+03 1.38166e-02
48 49 550 1.00000e+00 2.45116e+03 1.26736e-02
49 50 561 1.00000e+00 2.45116e+03 1.00676e-02
50 51 572 1.00000e+00 2.45116e+03 9.68540e-03
51 52 584 1.00000e+00 2.45116e+03 9.93275e-03
52 53 595 1.00000e+00 2.45116e+03 9.95888e-03
53 54 606 1.00000e+00 2.45116e+03 8.51003e-03
54 55 617 1.00000e+00 2.45116e+03 9.56613e-03
55 56 628 1.00000e+00 2.45116e+03 1.14717e-02
56 57 640 1.00000e+00 2.45116e+03 1.10797e-02
57 58 652 1.00000e+00 2.45116e+03 9.66020e-03
58 59 664 1.00000e+00 2.45116e+03 7.12239e-03
59 60 675 1.00000e+00 2.45116e+03 9.70268e-03
60 61 686 1.00000e+00 2.45116e+03 1.06271e-02
61 62 697 1.00000e+00 2.45116e+03 8.66663e-03
62 63 709 1.00000e+00 2.45116e+03 5.21659e-03
63 64 720 1.00000e+00 2.45116e+03 8.04831e-03
64 65 732 1.00000e+00 2.45116e+03 6.38215e-03
65 66 743 1.00000e+00 2.45116e+03 7.36685e-03
66 67 755 1.00000e+00 2.45116e+03 9.52317e-03
67 68 766 1.00000e+00 2.45116e+03 7.16611e-03
68 69 777 1.00000e+00 2.45116e+03 5.36047e-03
69 70 788 1.00000e+00 2.45116e+03 5.32784e-03
70 71 800 1.00000e+00 2.45116e+03 4.36776e-03
71 72 812 1.00000e+00 2.45116e+03 3.60682e-03
72 73 823 1.00000e+00 2.45116e+03 2.98529e-03
73 74 834 1.00000e+00 2.45116e+03 3.28175e-03
74 75 846 1.00000e+00 2.45116e+03 3.00937e-03
75 76 858 1.00000e+00 2.45116e+03 3.05478e-03
76 77 870 1.00000e+00 2.45116e+03 2.93148e-03
77 78 882 1.00000e+00 2.45116e+03 2.35747e-03
78 79 893 1.00000e+00 2.45116e+03 2.20906e-03
79 80 904 1.00000e+00 2.45116e+03 2.15725e-03
80 81 916 1.00000e+00 2.45116e+03 1.69084e-03
81 82 928 1.00000e+00 2.45116e+03 1.66883e-03
82 83 940 1.00000e+00 2.45116e+03 1.43711e-03
Directional Derivative below progTol
Number of non-zero variables associated with edge from 1 to 2: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 3: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 4: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 5: 80 (of 80)
Number of non-zero variables associated with edge from 1 to 6: 80 (of 80)
Number of non-zero variables associated with edge from 1 to 7: 80 (of 80)
Number of non-zero variables associated with edge from 1 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 1 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 1 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 1 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 3: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 4: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 5: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 6: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 7: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 9: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 14: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 16: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 2 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 2 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 4: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 5: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 6: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 7: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 13: 80 (of 80)
Number of non-zero variables associated with edge from 3 to 14: 80 (of 80)
Number of non-zero variables associated with edge from 3 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 3 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 5: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 6: 80 (of 80)
Number of non-zero variables associated with edge from 4 to 7: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 15: 80 (of 80)
Number of non-zero variables associated with edge from 4 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 17: 80 (of 80)
Number of non-zero variables associated with edge from 4 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 4 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 4 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 6: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 7: 80 (of 80)
Number of non-zero variables associated with edge from 5 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 5 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 5 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 7: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 6 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 8: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 9: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 11: 80 (of 80)
Number of non-zero variables associated with edge from 7 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 7 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 9: 80 (of 80)
Number of non-zero variables associated with edge from 8 to 10: 80 (of 80)
Number of non-zero variables associated with edge from 8 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 12: 80 (of 80)
Number of non-zero variables associated with edge from 8 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 8 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 10: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 11: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 14: 80 (of 80)
Number of non-zero variables associated with edge from 9 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 16: 80 (of 80)
Number of non-zero variables associated with edge from 9 to 17: 80 (of 80)
Number of non-zero variables associated with edge from 9 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 9 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 10 to 11: 80 (of 80)
Number of non-zero variables associated with edge from 10 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 10 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 10 to 14: 80 (of 80)
Number of non-zero variables associated with edge from 10 to 15: 80 (of 80)
Number of non-zero variables associated with edge from 10 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 10 to 17: 80 (of 80)
Number of non-zero variables associated with edge from 10 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 10 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 10 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 12: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 11 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 11 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 13: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 12 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 12 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 12 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 13 to 14: 0 (of 80)
Number of non-zero variables associated with edge from 13 to 15: 79 (of 80)
Number of non-zero variables associated with edge from 13 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 13 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 13 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 13 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 13 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 14 to 15: 0 (of 80)
Number of non-zero variables associated with edge from 14 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 14 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 14 to 18: 0 (of 80)
Number of non-zero variables associated with edge from 14 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 14 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 15 to 16: 0 (of 80)
Number of non-zero variables associated with edge from 15 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 15 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 15 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 15 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 16 to 17: 0 (of 80)
Number of non-zero variables associated with edge from 16 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 16 to 19: 80 (of 80)
Number of non-zero variables associated with edge from 16 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 17 to 18: 80 (of 80)
Number of non-zero variables associated with edge from 17 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 17 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 18 to 19: 0 (of 80)
Number of non-zero variables associated with edge from 18 to 20: 0 (of 80)
Number of non-zero variables associated with edge from 19 to 20: 0 (of 80)
neato - Graphviz version 2.20.2 (Tue Mar 2 19:03:41 UTC 2010)