Examples of using minConf_QNST

These demos have been set up to show how minConf_QNST from the thesis code package can be used to optimize the sum of a smooth function and a variety of simple non-smooth functions. The code uses a simultaneous linear regression loss which has a matrix of parameters, but any smooth loss and vectorized parameter-structure can be used in its place.

The code used to run these demos can be downloaded here (which includes a copy of the 2012 version of the minConf and L1GeneralGroup codes from the thesis package as well as the 2012 version of minFunc package).

To run all of the demos, type (in Matlab): 

>> cd QNSTexamples           % Change to the extracted directory
>> addpath(genpath(pwd))     % Add all sub-directories to the Matlab path
>> mexAll                    % Compile mex files (not necessary on all systems)
>> QNST_examples             % Run the examples

Contents

L1-Regularization

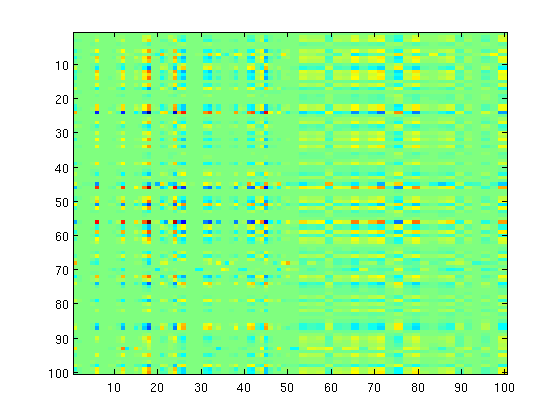
We first solve min_W |X*W - Y|_F^2 + lambda*sum_{ij}|W_{ij}|.

n = 500;
p = 100;
k = 50;
X = randn(n,p);
W = diag(rand(p,1) > .9)*randn(p,k) + randn(p,1)*randn(1,k);
Y = X*W + randn(n,k);

% Smooth Part of Objective Function
funObj1 = @(W)SimultaneousSquaredError(W,X,Y);

% Non-Smooth Part
lambda = 500;
funObj2 = @(W)lambda*sum(abs(W));

% Prox Operator
funProx = @(W,alpha)sign(W).*max(abs(W)-lambda*alpha,0);

% Optimize with QNST
fprintf('Optimizing with L1-regularization\n');
W(:) = minConf_QNST(funObj1,funObj2,W(:),funProx);

imagesc(W);
sparsityW = nnz(W)
rowSparsityW = nnz(sum(abs(W),2))
rankW = rank(W)
pause

Optimizing with L1-regularization
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     5.67600e-06     1.70587e+06     7.04377e+00
         2          3         14     1.00000e+00     1.22290e+06     3.65143e+02
         3          4         25     1.00000e+00     1.21050e+06     2.76634e+02
         4          5         36     1.00000e+00     1.20843e+06     5.63210e+01
         5          6         47     1.00000e+00     1.20819e+06     1.51310e+01
         6          7         58     1.00000e+00     1.20815e+06     1.31426e+01
         7          8         69     1.00000e+00     1.20815e+06     1.05438e+01
         8          9         80     1.00000e+00     1.20815e+06     1.20435e+00
         9         10         91     1.00000e+00     1.20815e+06     7.22492e-01
        10         11        102     1.00000e+00     1.20815e+06     3.48033e-01
        11         12        113     1.00000e+00     1.20815e+06     2.94417e-01
        12         13        124     1.00000e+00     1.20815e+06     4.28418e-02
        13         14        135     1.00000e+00     1.20815e+06     2.75246e-02
        14         15        146     1.00000e+00     1.20815e+06     7.57646e-03
        15         16        156     1.00000e+00     1.20815e+06     1.16867e-02
        16         17        167     1.00000e+00     1.20815e+06     1.05576e-03
        17         18        178     1.00000e+00     1.20815e+06     7.62134e-04
Backtracking
Backtracking
Backtracking
        18         22        180     1.25000e-01     1.20815e+06     7.62130e-04
Step size below progTol

sparsityW =

        2115


rowSparsityW =

    81


rankW =

    46

Group L_{1,2}-Regularization

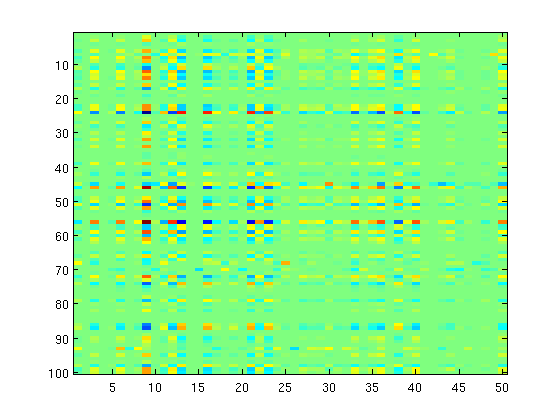
We now replace the L1-norm regularizer with the group-L1 regularizer, lambda*sum_g |W_g|_2, where in this case we will define the groups 'g' as the rows of the matrix (so each group penalizes an original input feature across the tasks)

% Non-Smooth part
groups = repmat([1:p]',1,k);
nGroups = p;
lambda = 5000*ones(nGroups,1);
funObj2 = @(w)groupL12regularizer(w,lambda,groups);

% Prox operator
funProx = @(w,alpha)groupSoftThreshold(w,alpha,lambda,groups);

% Optimize with QNST
fprintf('Optimizing with Group L1-regularization\n');
W(:) = minConf_QNST(funObj1,funObj2,W(:),funProx);

imagesc(W);
sparsityW = nnz(W)
rowSparsityW = nnz(sum(abs(W),2))
rankW = rank(W)
pause

Optimizing with Group L1-regularization
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     6.21419e-07     2.18153e+06     6.32939e+00
         2          3         14     1.00000e+00     1.87914e+06     2.89786e+02
         3          4         25     1.00000e+00     1.87331e+06     1.67806e+02
         4          5         36     1.00000e+00     1.87231e+06     3.97104e+01
         5          6         47     1.00000e+00     1.87222e+06     1.21644e+01
         6          7         58     1.00000e+00     1.87221e+06     3.98087e+00
         7          8         69     1.00000e+00     1.87221e+06     1.27334e+00
         8          9         80     1.00000e+00     1.87221e+06     3.75560e-01
         9         10         91     1.00000e+00     1.87221e+06     2.72207e-01
        10         11        102     1.00000e+00     1.87221e+06     4.75585e-02
        11         12        113     1.00000e+00     1.87221e+06     1.88721e-02
        12         13        124     1.00000e+00     1.87221e+06     4.19713e-03
        13         14        133     1.00000e+00     1.87221e+06     1.03279e-03
        14         15        140     1.00000e+00     1.87221e+06     5.15932e-04
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
        15         21        144     3.12500e-02     1.87221e+06     5.01335e-04
Backtracking
        16         23        153     5.00000e-01     1.87221e+06     2.78746e-04
Backtracking
Backtracking
Backtracking
        17         27        155     1.25000e-01     1.87221e+06     2.78725e-04
Step size below progTol

sparsityW =

        2650


rowSparsityW =

    53


rankW =

    50

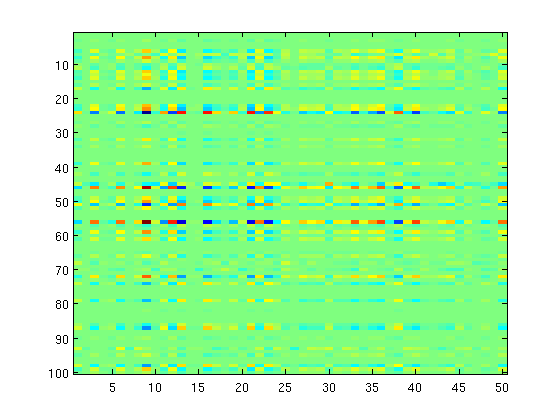
Group L_{1,inf}-Regularization

We now replacethe L2-norm in the group L1-regularizer by the infinity-norm

% Non-Smooth Part
lambda = 20000*ones(nGroups,1);
funObj2 = @(w)groupL1infregularizer(w,lambda,groups);

% Prox operator
funProx = @(w,alpha)groupInfSoftThreshold(w,alpha,lambda,groups);

% Optimize with QNST
fprintf('Optimizing with L1-regularization (inf-norm of groups)\n');
W(:) = minConf_QNST(funObj1,funObj2,W(:),funProx);

imagesc(W);
sparsityW = nnz(W)
rowSparsityW = nnz(sum(abs(W),2))
rankW = rank(W)
pause

Optimizing with L1-regularization (inf-norm of groups)
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     4.64665e-07     2.29495e+06     2.14030e+02
         2          3         14     1.00000e+00     1.71497e+06     5.72119e+01
         3          4         25     1.00000e+00     1.71291e+06     2.44158e+01
         4          5         36     1.00000e+00     1.71259e+06     1.43311e+01
         5          6         47     1.00000e+00     1.71256e+06     6.34727e+00
         6          7         58     1.00000e+00     1.71256e+06     2.05939e+00
         7          8         69     1.00000e+00     1.71256e+06     9.31368e-01
         8          9         80     1.00000e+00     1.71256e+06     2.95674e-01
         9         10         91     1.00000e+00     1.71256e+06     8.64231e-02
        10         11        102     1.00000e+00     1.71256e+06     7.24820e-02
        11         12        113     1.00000e+00     1.71256e+06     9.37750e-03
        12         13        124     1.00000e+00     1.71256e+06     4.38607e-03
        13         14        135     1.00000e+00     1.71256e+06     1.35396e-03
        14         15        146     1.00000e+00     1.71256e+06     1.11289e-03
        15         16        156     1.00000e+00     1.71256e+06     1.29581e-04
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
        16         22        158     3.12500e-02     1.71256e+06     1.29580e-04
Step size below progTol

sparsityW =

        3100


rowSparsityW =

    62


rankW =

    41

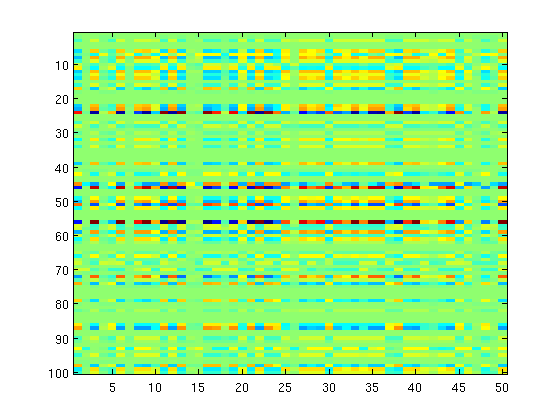
Combined L1- and Group L1-Regularization

We now consider applying both the group L1-regularizer to select rows, and the regular L1-regularizer to select within the rows

% Non-Smooth Part
lambda1 = 500;
lambda2 = 5000*ones(nGroups,1);
funObj2 = @(w)lambda1*sum(abs(w)) + groupL12regularizer(w,lambda2,groups);

% Prox operator
funProx1 = @(w,alpha,lambda1)sign(w).*max(abs(w)-lambda1*alpha,0);
funProx = @(w,alpha)groupSoftThreshold(funProx1(w,alpha,lambda1),alpha,lambda2,groups);

% Optimize with QNST
fprintf('Optimizing with combined L1- and group L1-regularization\n');
W(:) = minConf_QNST(funObj1,funObj2,W(:),funProx);

imagesc(W);
sparsityW = nnz(W)
rowSparsityW = nnz(sum(abs(W),2))
rankW = rank(W)
pause

Optimizing with combined L1- and group L1-regularization
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     6.05320e-07     2.89417e+06     2.91697e+00
         2          3         14     1.00000e+00     2.27797e+06     3.83235e+02
         3          4         25     1.00000e+00     2.27383e+06     1.64033e+02
         4          5         36     1.00000e+00     2.27348e+06     2.46806e+01
         5          6         47     1.00000e+00     2.27347e+06     4.04257e+00
         6          7         58     1.00000e+00     2.27347e+06     1.23466e+00
         7          8         69     1.00000e+00     2.27347e+06     2.85872e-01
         8          9         80     1.00000e+00     2.27347e+06     8.26774e-02
         9         10         91     1.00000e+00     2.27347e+06     1.57977e-02
        10         11        102     1.00000e+00     2.27347e+06     3.13227e-03
        11         12        111     1.00000e+00     2.27347e+06     8.00092e-04
        12         13        113     1.00000e+00     2.27347e+06     7.99920e-04
Step size below progTol

sparsityW =

        1233


rowSparsityW =

    33


rankW =

    33

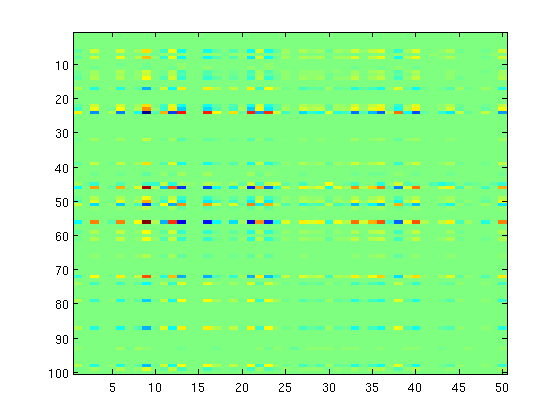
Nuclear norm-regularization

% Non-Smooth Part
lambda = 1000;
toMat = @(w)reshape(w,p,k);
funObj2 = @(w)lambda*sum(svd(toMat(w)));

% Prox Operator
funProx = @(w,alpha)traceSoftThreshold(w,alpha,lambda,p,k);

% Optimize with QNST
fprintf('Optimizing with Nuclear norm-regularization\n');
W(:) = minConf_QNST(funObj1,funObj2,W(:),funProx);

imagesc(W);
sparsityW = nnz(W)
rowSparsityW = nnz(sum(abs(W),2))
rankW = rank(W)
pause

Optimizing with Nuclear norm-regularization
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     3.37433e-07     1.51860e+06     2.80965e+03
         2          3         14     1.00000e+00     1.77268e+05     6.46726e+02
         3          4         25     1.00000e+00     1.42941e+05     2.87792e+02
         4          5         36     1.00000e+00     1.29280e+05     1.76148e+02
         5          6         47     1.00000e+00     1.27260e+05     1.01399e+02
         6          7         58     1.00000e+00     1.26250e+05     1.20974e+01
         7          8         69     1.00000e+00     1.26170e+05     6.51647e+00
         8          9         80     1.00000e+00     1.26113e+05     1.51745e+00
Backtracking
         9         11         91     5.00000e-01     1.26112e+05     1.43713e+00
        10         12        102     1.00000e+00     1.26111e+05     4.42353e-01
        11         13        113     1.00000e+00     1.26111e+05     5.31571e-02
        12         14        124     1.00000e+00     1.26111e+05     4.45863e-02
        13         15        135     1.00000e+00     1.26111e+05     6.07540e-02
        14         16        146     1.00000e+00     1.26111e+05     1.11414e-02
        15         17        157     1.00000e+00     1.26111e+05     4.53048e-03
        16         18        167     1.00000e+00     1.26111e+05     2.25357e-03
        17         19        177     1.00000e+00     1.26111e+05     1.69649e-03
Backtracking
        18         21        186     5.00000e-01     1.26111e+05     1.07237e-03
        19         22        194     1.00000e+00     1.26111e+05     2.12208e-04
        20         23        196     1.00000e+00     1.26111e+05     2.11143e-04
Function value changing by less than progTol

sparsityW =

        5000


rowSparsityW =

   100


rankW =

     6

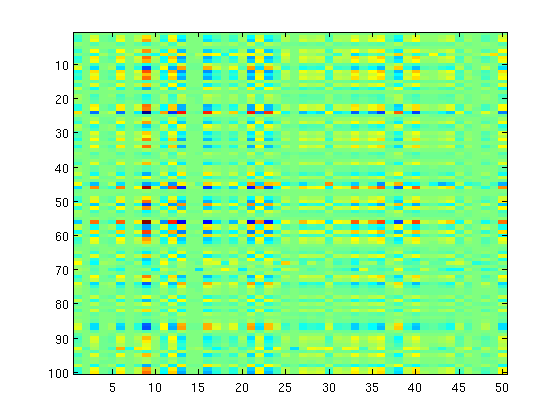
Sparse plus low-rank

% Smooth Part
funObj1 = @(ww)SimultaneousSquaredError(ww,[X X],Y);

% Non-Smooth Part
lambda1 = 500;
lambdaT = 1000;
funObj2 = @(ww)lambda1*sum(abs(ww(1:end/2))) + lambdaT*sum(svd(toMat(ww(end/2+1:end))));

% Prox Operator
fprintf('Optimizing with an L1-regularized matrix plus a nuclear norm-regularized matrix\n');
funProx = @(ww,alpha)[funProx1(ww(1:end/2),alpha,lambda1);traceSoftThreshold(ww(end/2+1:end),alpha,lambdaT,p,k)];

% Optimize with QNST
WW = [W W];
WW(:) = minConf_QNST(funObj1,funObj2,WW(:),funProx);
W1 = WW(:,1:k);
W2 = WW(:,k+1:end);

imagesc([W1 W2]);
sparsityWW = [nnz(W1) nnz(W2)]
rowSparsityWW = [nnz(sum(abs(W1),2)) nnz(sum(abs(W2),2))]
rankWW = [rank(W1) rank(W2)]
pause

Optimizing with an L1-regularized matrix plus a nuclear norm-regularized matrix
 Iteration   FunEvals Projections     Step Length    Function Val
         1          2          3     7.47806e-08     1.02239e+07     1.02872e+04
         2          3         14     1.00000e+00     1.60293e+06     1.19224e+03
         3          4         25     1.00000e+00     1.22249e+06     6.87262e+02
         4          5         36     1.00000e+00     9.03344e+05     3.12295e+02
         5          6         47     1.00000e+00     8.32055e+05     2.85429e+02
         6          7         58     1.00000e+00     8.06425e+05     2.84796e+02
         7          8         69     1.00000e+00     7.93099e+05     1.98060e+02
         8          9         80     1.00000e+00     7.87747e+05     1.18403e+02
         9         10         91     1.00000e+00     7.85998e+05     1.35948e+02
        10         11        102     1.00000e+00     7.84634e+05     2.19619e+02
        11         12        113     1.00000e+00     7.83355e+05     3.24916e+02
        12         13        124     1.00000e+00     7.81481e+05     2.94150e+02
        13         14        135     1.00000e+00     7.79444e+05     7.03009e+01
        14         15        146     1.00000e+00     7.77462e+05     7.38736e+01
        15         16        157     1.00000e+00     7.75583e+05     8.47324e+01
        16         17        168     1.00000e+00     7.73826e+05     8.51363e+01
        17         18        179     1.00000e+00     7.72077e+05     9.45061e+01
        18         19        190     1.00000e+00     7.70087e+05     9.26096e+01
        19         20        201     1.00000e+00     7.68388e+05     1.22484e+02
        20         21        212     1.00000e+00     7.67151e+05     9.23538e+01
        21         22        223     1.00000e+00     7.65928e+05     4.04646e+01
        22         23        234     1.00000e+00     7.64895e+05     1.02808e+01
        23         24        245     1.00000e+00     7.64092e+05     1.18743e+01
        24         25        256     1.00000e+00     7.63502e+05     1.08929e+01
        25         26        267     1.00000e+00     7.63202e+05     1.22638e+01
        26         27        278     1.00000e+00     7.63001e+05     1.21021e+01
        27         28        289     1.00000e+00     7.62805e+05     1.03173e+01
        28         29        300     1.00000e+00     7.62701e+05     3.39680e+00
        29         30        311     1.00000e+00     7.62627e+05     2.43321e+00
        30         31        322     1.00000e+00     7.62580e+05     1.71668e+00
        31         32        333     1.00000e+00     7.62537e+05     1.72409e+00
        32         33        344     1.00000e+00     7.62503e+05     1.45140e+00
        33         34        355     1.00000e+00     7.62481e+05     1.42317e+00
        34         35        366     1.00000e+00     7.62466e+05     1.94852e+00
        35         36        377     1.00000e+00     7.62455e+05     1.36560e+00
        36         37        388     1.00000e+00     7.62446e+05     6.64757e-01
        37         38        399     1.00000e+00     7.62442e+05     5.08786e-01
        38         39        410     1.00000e+00     7.62439e+05     5.18427e-01
        39         40        421     1.00000e+00     7.62437e+05     3.08529e-01
        40         41        432     1.00000e+00     7.62435e+05     1.57779e-01
        41         42        443     1.00000e+00     7.62434e+05     1.53342e-01
        42         43        454     1.00000e+00     7.62434e+05     1.09305e-01
        43         44        465     1.00000e+00     7.62433e+05     4.55714e-02
        44         45        476     1.00000e+00     7.62433e+05     4.58755e-02
        45         46        487     1.00000e+00     7.62433e+05     5.75640e-02
        46         47        498     1.00000e+00     7.62433e+05     3.34557e-02
        47         48        509     1.00000e+00     7.62433e+05     3.34345e-02
        48         49        520     1.00000e+00     7.62433e+05     3.42765e-02
        49         50        531     1.00000e+00     7.62433e+05     2.96381e-02
        50         51        542     1.00000e+00     7.62433e+05     2.00916e-02
        51         52        553     1.00000e+00     7.62433e+05     1.59632e-02
        52         53        564     1.00000e+00     7.62433e+05     1.85411e-02
        53         54        575     1.00000e+00     7.62433e+05     1.61407e-02
        54         55        586     1.00000e+00     7.62433e+05     1.06767e-02
        55         56        597     1.00000e+00     7.62433e+05     4.99576e-03
        56         57        608     1.00000e+00     7.62433e+05     3.10343e-03
        57         58        619     1.00000e+00     7.62433e+05     1.81558e-03
        58         59        630     1.00000e+00     7.62433e+05     1.50687e-03
        59         60        641     1.00000e+00     7.62433e+05     7.05088e-04
        60         61        651     1.00000e+00     7.62433e+05     1.23841e-03
        61         62        662     1.00000e+00     7.62433e+05     9.24279e-04
        62         63        673     1.00000e+00     7.62433e+05     4.23286e-04
        63         64        684     1.00000e+00     7.62433e+05     6.35501e-04
        64         65        695     1.00000e+00     7.62433e+05     6.34014e-04
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
Backtracking
        65         74        697     3.90625e-03     7.62433e+05     6.34013e-04
Step size below progTol

sparsityWW =

        2200        5000


rowSparsityWW =

    81   100


rankWW =

    43     6


Published with MATLAB® 7.14

Mark Schmidt > Software > thesis > Examples of using minConf_QNST