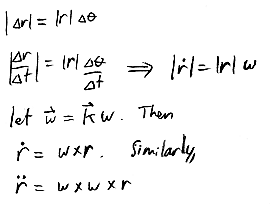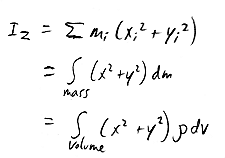Introduction to Rigid Body Dynamics

Preliminaries

Cross product review

• a x a = 0
• a x b is perpendicular to both a and b.


• right hand rule: if the fingers are curled from a to b, the thumb points in the direction of a x b
• a x b as a matrix product:


• note:

a x a = 0
a x b = - b x a
a x (b+c) = axb + axc

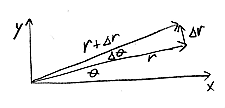
Kinematics of 2D rotation

• determine the velocity and acceleration of a rotating point

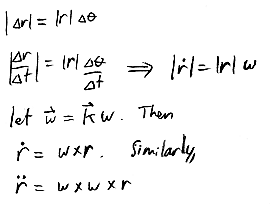
Newton's 2nd law

• linear momentum:   P = m v
• Newton's 2nd law:


• conservation of linear momentum


• inertial frame:  a coordinate frame in which Newton's second law holds
• all intertial frames can be related to a universal frame
• intertial frames do not accelerate or rotate with respect to the universal frame

Center of mass

• consider a rigid system of particles:

• Newton's 2nd law applied to the individual particles:


• Newton's 2nd law applied to the ensemble:

Rotation

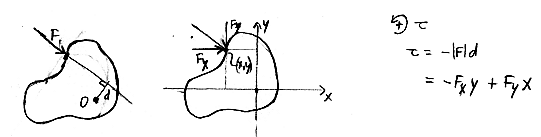
• intuition:   torques are 'angular forces'


• example:  rotation about a fixed axis


• computing work as being the product of force and distance:


• re-express the work in terms of the product of torque and angle


• geometry of computing torques

Angular Momentum

• recall that the sum of forces equals the rate of change of linear momentum


• similarly, the sum of torques equals the rate of change of angular momentum


• consider one particle


• consider a rigid system of particles


• conservation of angular momentum


• example 1: consider a planet with an elliptical orbit


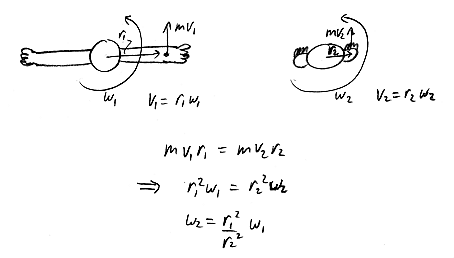
• example 2: figure skater

Moment of inertia

• consider an object rotating about a fixed axis O:


• revisiting the figure skater:


decreasing the moment of inertia increases the spinning speed
• computing I

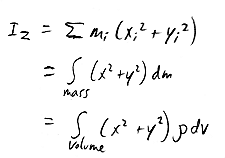
Kinetic Energy

• for a body which is not rotating:


• for a body which is only rotating: