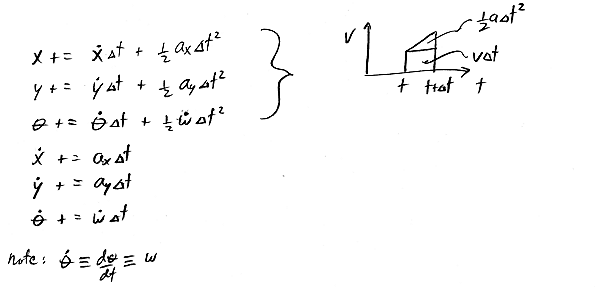Simulating Rigid Body Dynamics

Newton-Euler equations of motion

• linear momentum


• angular momentum


• Note: only valid in the intertial frame!
• equations of motion

Simulation of a single rigid body in a planar world

• Newton-Euler equations


• integration

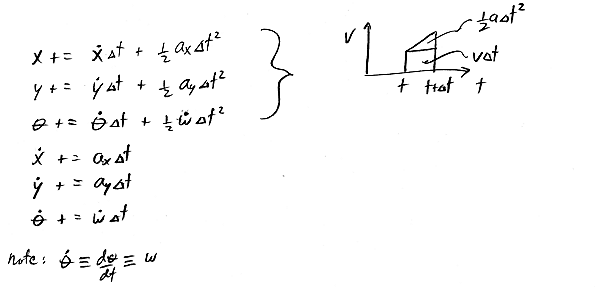
Simulation of two rigid bodies with a hinge in a planar world

Formulation using redundant coordinates (A)

• introduce extra unknown


• introduce extra equation


• For the above equation we need an expression for the acceleration of a point on a rotating rigid body


• equations of motion


• placing the equations in matrix form gives:

Correcting joint drift in redundant coordinates

numerical integration errors will accumulate over time

introduce a virtual corrective force to combat drift

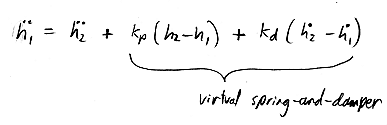
Simulation of a 5-link chain

consider a 5-link chain in 2D or 3D

• using redundant coordinates, we will need to introduce 5 unknown forces, corresponding to the 5 hinges
• five corresponding acceleration equations are also required to enforce the attachment constraints at the hinges
• this yields the following matrix structure:

Formulation using reduced coordinates (B)

• consider simulating the same two-link configuration using reduced coordinates: