Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).

9.2 One-Off Decisions

Basic decision theory applied to intelligent agents relies on the following assumptions:

  • Agents know what actions they can carry out.
  • The effect of each action can be described as a probability distribution over outcomes.
  • An agent's preferences are expressed by utilities of outcomes.

It is a consequence of Proposition 9.1 that, if agents only act for one step, a rational agent should choose an action with the highest expected utility.

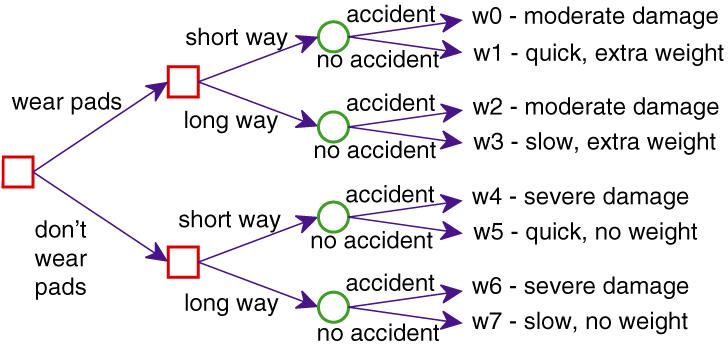
figures/ch09/DT-accidentc.gif
Figure 9.4: A decision tree for the delivery robot. Square boxes represent decisions that the robot can make. Circles represent random variables that the robot cannot observe before making its decision.
Example 9.4: Consider the problem of the delivery robot in which there is uncertainty in the outcome of its actions. In particular, consider the problem of going from position o109 in Figure 3.1 to the mail position, where there is a chance that the robot will slip off course and fall down the stairs. Suppose the robot can get pads that will not change the probability of an accident but will make an accident less severe. Unfortunately, the pads add extra weight. The robot could also go the long way around, which would reduce the probability of an accident but make the trip much slower.

Thus, the robot has to decide whether to wear the pads and which way to go (the long way or the short way). What is not under its direct control is whether there is an accident, although this probability can be reduced by going the long way around. For each combination of the agent's choices and whether there is an accident, there is an outcome ranging from severe damage to arriving quickly without the extra weight of the pads.

To model one-off decision making, a decision variable can be used to model an agent's choice. A decision variable is like a random variable, with a domain, but it does not have an associated probability distribution. Instead, an agent gets to choose a value for a decision variable. A possible world specifies values for both random and decision variables, and for each combination of values to decision variables, there is a probability distribution over the random variables. That is, for each assignment of a value to each decision variable, the measures of the worlds that satisfy that assignment sum to 1. Conditional probabilities are only defined when a value for every decision variable is part of what is conditioned on.

Figure 9.4 shows a decision tree that depicts the different choices available to the agent and their outcomes. [These are different from the decision trees used for classification]. To read the decision tree, start at the root (on the left in this figure). From each node one of the branches can be followed. For the decision nodes, shown as squares, the agent gets to choose which branch to take. For each random node, shown as a circle, the agent does not get to choose which branch will be taken; rather there is a probability distribution over the branches from that node. Each path to a leaf corresponds to a world, shown as wi, which is the outcome that will be true if that path is followed.

Example 9.5: In Example 9.4 there are two decision variables, one corresponding to the decision of whether the robot wears pads and one to the decision of which way to go. There is one random variable, whether there is an accident or not. Eight possible worlds exist, corresponding to the eight paths in the decision tree of Figure 9.4.

What the agent should do depends on how important it is to arrive quickly, how much the pads' weight matters, how much it is worth to reduce the damage from severe to moderate, and the likelihood of an accident.

The proof of Proposition 9.1 specifies how to measure the desirability of the outcomes. Suppose we decide to have utilities in the range [0,100]. First, choose the best outcome, which would be w5, and give it a utility of 100. The worst outcome is w6, so assign it a utility of 0. For each of the other worlds, consider the lottery between w6 and w5. For example, w0 may have a utility of 35, meaning the agent is indifferent between w0 and [0.35 : w5, 0.65:w6], which is slightly better than w2, which may have a utility of 30. w1 may have a utility of 95, because it is only slightly worse than w5.

Example 9.6: In diagnosis, decision variables correspond to various treatments and tests. The utility may depend on the costs of tests and treatment and whether the patient gets better, stays sick, or dies, and whether they have short-term or chronic pain. The outcomes for the patient depend on the treatment the patient receives, the patient's physiology, and the details of the disease, which may not be known with certainty. Although we have used the vocabulary of medical diagnosis, the same approach holds for diagnosis of artifacts such as airplanes.

In a one-off decision, the agent chooses a value for each decision variable. This can be modeled by treating all the decision variables as a single composite decision variable. The domain of this decision variable is the cross product of the domains of the individual decision variables. Call the resulting composite decision variable D.

Each world ω specifies an assignment of a value to the decision variable D and an assignment of a value to each random variable.

A single decision is an assignment of a value to the decision variable. The expected utility of single decision D=di is

E(U|D=di) = ∑ω |= (D=di) U(ω)×P(ω),

where P(ω) is the probability of world ω, and U(ω) is the value of the utility U in world ω; ω |= (D=di) means that the decision variable D has value di in world ω. Thus, the expected-utility computation involves summing over the worlds that select the appropriate decision.

An optimal single decision is the decision whose expected utility is maximal. That is, D=dmax is an optimal decision if

E(U|D=dmax)=maxdi∈dom(D)E(U|D=di),

where dom(D) is the domain of decision variable D. Thus,

dmax=argmaxdi∈dom(D)E(U|D=di).
Example 9.7: The delivery robot problem of Example 9.4 is a single decision problem where the robot has to decide on the values for the variables Wear_Pads and Which_Way. The single decision is the complex decision variable ⟨Wear_Pads,Which_Way⟩. Each assignment of a value to each decision variable has an expected value. For example, the expected utility of Wear_Pads=true∧Which_Way=short is given by
E(U|wear_pads∧Which_Way=short)
      = P(accident |wear_pads∧Which_way=short) ×utility(w0)
      +(1-P(accident |wear_pads∧Which_way=short)) ×utility(w1),

where the worlds w0 and w1 are as in Figure 9.4, and wear_pads means Wear_Pads=true.